KL距离,是Kullback-Leibler差异(Kullback-Leibler Divergence)的简称,也叫做相对熵(Relative Entropy)。它衡量的是相同事件空间里的两个概率分布的差异情况。
KL距离全称为Kullback-Leibler Divergence,也被称为相对熵。公式为:
感性的理解,KL距离可以解释为在相同的事件空间P(x)中两个概率P(x)和Q(x)分布的差异情况。
从其物理意义上分析:可解释为在相同事件空间里,概率分布P(x)的事件空间,若用概率分布Q(x)编码时,平均每个基本事件(符号)编码长度增加了多少比特。
如上面展开公式所示,前面一项是在P(x)概率分布下的熵的负数,而熵是用来表示在此概率分布下,平均每个事件需要多少比特编码。这样就不难理解上述物理意义的编码的概念了。
但是KL距离并不是传统意义上的距离。传统意义上的距离需要满足三个条件:1)非负性;2)对称性(不满足);3)三角不等式(不满足)。但是KL距离三个都不满足。反例可以看参考资料中的例子。
+++++++++++++++++++++++++++++++++++++++++++++++++++
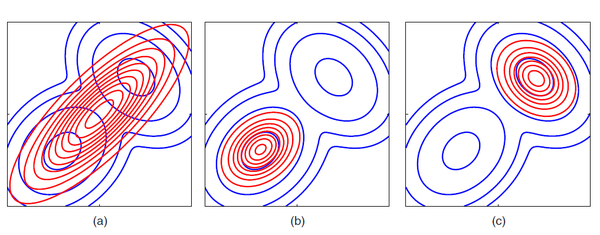
作者:肖天睿链接:https://www.zhihu.com/question/29980971/answer/93489660来源:知乎著作权归作者所有,转载请联系作者获得授权。Interesting question, KL divergence is something I'm working with right now.KL divergence KL(p||q), in the context of information theory, measures the amount of extra bits (nats) that is necessary to describe samples from the distribution p with coding based on q instead of p itself. From the Kraft-Macmillan theorem, we know that the coding scheme for one value out of a set X can be represented q(x) = 2^(-l_i) as over X, where l_i is the length of the code for x_i in bits.We know that KL divergence is also the relative entropy between two distributions, and that gives some intuition as to why in it's used in variational methods. Variational methods use functionals as measures in its objective function (i.e. entropy of a distribution takes in a distribution and return a scalar quantity). It's interpreted as the "loss of information" when using one distribution to approximate another, and is desirable in machine learning due to the fact that in models where dimensionality reduction is used, we would like to preserve as much information of the original input as possible. This is more obvious when looking at VAEs which use the KL divergence between the posterior q and prior p distribution over the latent variable z. Likewise, you can refer to EM, where we decomposeln p(X) = L(q) + KL(q||p)Here we maximize the lower bound on L(q) by minimizing the KL divergence, which becomes 0 when p(Z|X) = q(Z). However, in many cases, we wish to restrict the family of distributions and parameterize q(Z) with a set of parameters w, so we can optimize w.r.t. w.Note that KL(p||q) = - \sum p(Z) ln (q(Z) / p(Z)), and so KL(p||q) is different from KL(q||p). This asymmetry, however, can be exploited in the sense that in cases where we wish to learn the parameters of a distribution q that over-compensates for p, we can minimize KL(p||q). Conversely when we wish to seek just the main components of p with q distribution, we can minimize KL(q||p). This example from the Bishop book illustrates this well.