看这篇文章之前，请确保你有基本的前端知识，知道Canvas最基本的使用方法,知道贝塞尔曲线在CSS3中的使用。本文章忽略了贝塞尔曲线的历史，不了解可自行谷歌百度。
三次贝塞尔曲线方程
推导过程
先看一下贝塞尔曲线的生成方法
二次贝塞尔曲线
三次贝塞尔曲线
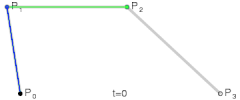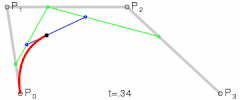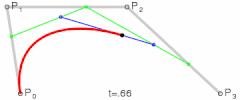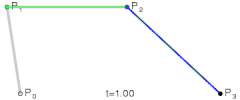Cubic Bezier Curve
四次贝塞尔曲线
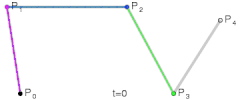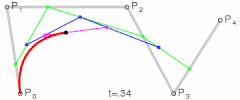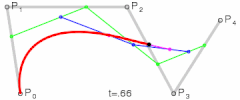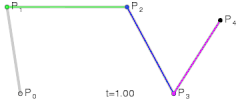
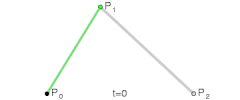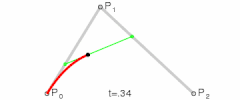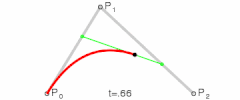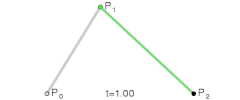
这是二次贝塞尔曲线、三次贝塞尔曲线、以及四次贝塞尔曲线的生成示意图，我们可以用平实的文字总结一下这些图形表达的含义:对于给定的曲线起点与终点以及一系列控制点，分别将起点与第一控制点，第一控制点与第二控制点，以此类推直至最后一个控制点与终点相连，然后分别将这些线段对应的相同比例部分的点相连，记此比例为t，再将这些二次连线上t位置的点相连，依次类推直到不存在第二条线段，最后这条线段t位置上的点就在贝塞尔曲线上，而当t∈[0,1]时这些点的集合就是贝塞尔曲线本身。
三次贝塞尔曲线就是如此计算的:
Q0:P0 + (P1-P0)t Q1:P1 + (P2-P1)t Q2:P2 + (P3-P2)t
A0:Q0 + (Q1-Q0)t A1:Q1 + (Q2-Q1)t
B(t) = A0 + (A1-A0)t
将所有点换成使用P0P1P2P3的表达式进行化简，即可化简为
B(t) = P0(1-t)³ + 3P1t(1-t)² + 3P2t²(1-t) + P3t³
化简过程涉及到换元，目的是抽象贝塞尔曲线的通用表达式，所以结果不是那么直观，不过这些都是数学细节，感兴趣可以去维基百科，平常接触最多的就是三次贝塞尔曲线，所以我们这里着重探讨的就是特殊的三次贝塞尔曲线而非普遍结论。
这一表达式中的变量t就是我们说的“各条线段上的比例”,在这里我们直接使用了一个字面量(如P0)来表示一个点，实际上编程时我们会将点分成xy坐标分别进行计算。
这里我将贝塞尔曲线的生成方法实现成了一个使用canvas绘制的过程例子，你可以直接拖动滑块改变描线速度。
运动位置计算
给定t拿到运动位置并非难事，因为我们已经有了曲线对应的函数表达式，直接代入参数t即可求得x,y坐标。
比如目前我们希望让物体位于某已知贝塞尔曲线的t位置，则我们需要的位置为
var x = P0x(1-t)³ + 3P1xt(1-t)² + 3P2xt²(1-t) + P3xt³;
var y = P0y(1-t)³ + 3P1yt(1-t)² + 3P2yt²(1-t) + P3yt³;
// position handler , e.g.
// oBox.style.transform = `translate(${x}px,${y}px)`;
当然，这里我们要注意的是：我们并没有在时间维度控制动画，或者说目前这个沿曲线运动的圆目前能做到的也仅仅是“沿着曲线运动”,我们目前还没有控制它的匀速、加速等速度模式。
Canvas任意曲线描线动画
想要实现canvas描线动画，首先我们应该知道canvas动画的实现方式:不断的绘制与擦除。既然我们需要的是一个描线动画，那么我们就可以将研究目标转向另一个问题:如何绘制从起始点开始到达三次贝塞尔曲线上给定一点的曲线线段？
实际上，我们已经知道了如何绘制三次贝塞尔曲线:不断运动的点所构成的线，那我们已经知道了t的位置，那实际上就是已经知道了绘制到给定点时对应的Q0,Q1,A0，而Q0与A0就是这段贝塞尔曲线的控制点，而B2便是终点值。
上文中演示贝塞尔曲线的生成就使用了这一方法，点击查看例子与源码
CSS3属性的转化
想知道如何将CSS3中的属性值转化为JS中的描述逻辑，首先应该搞清楚CSS3中的贝塞尔曲线表达式到底是什么。
- 属性值的含义
我们看到的CSS3中无论是 transition-timing-function 还是 animation-timing-function都是可以支持三次贝塞尔曲线表达式的，形如cubic-bezier(0.2,0.3,0.71,0.43)，括号内有四个值，我们之前了解到的三次贝塞尔曲线相关的点需要四个：起点，第一控制点，第二控制点，终点，而我们的CSS3运动函数的三次贝塞尔曲线表达式把起点与终点分别约定为(0,0)与(1,1)，所以我们这个括号里传的四个参数分别是第一、二控制点的X坐标、y坐标，即为
cubic-bezier( P1x, P1y, P2x, P2y)
那既然如此我们就清楚了：我们三次函数表达式中需要的数据都齐全了,下面仅需将CSS表达式转化成JS表达式就好，我们的方法接受CSS3贝塞尔曲线表达式，返回值为接受x为参数返回值为对应y值的方法。
点击查看CSS属性转化
本例子实现了以下效果:将CSS3的属性转化成对应的三次贝塞尔曲线。那现在有一个问题：我们如何使用这个贝塞尔曲线作为我们所做动画的时间变化函数？
时间比例函数
实际上，我们在这里有三个变量:t,x,y，根据t与四个已知点我们可以获得对应点的xy值，但是这个等式对我们使用它作为时间函数并没有任何作用，我们需要的是：将x作为自变量匀速递增，这时的x的物理意义便是运动时间，而x值在贝塞尔曲线上对应的点的y坐标的意义便是物体运动的百分比。那么我们目前面临的问题便是：给定一个x，如何在某个特定的贝塞尔曲线上计算出对应的y值？
实际上我们是没有办法直接算出y的，根据我们已知的函数方程
x = P0x(1-t)³ + 3P1xt(1-t)² + 3P2xt²(1-t) + P3xt³ (1)
y = P0y(1-t)³ + 3P1yt(1-t)² + 3P2yt²(1-t) + P3yt³ (2)
在这两个函数表达式中我们已知的变量只有x，所以我们只能通过(1)式反求出此时的比例t，然后再代入(2)式获取y值。
因为P0P1P2P3都是已知量，将(1)式简化后是一个t相关的一元三次函数：
at³ + bt² + ct + d = 0 // 此多项式为由上式合并同类项后得出，参数为合并后代数值
也就是说我们目前已知a,b,c,d,求出t值，并且我们知道t值的取值范围是t∈[0,1],所以解三次方程就可以得出了。
但是在实践中有个问题：解三次函数会涉及到大量的开方相除操作，并没有现成的解三次方函数。这里需要一些计算机求值方面的技巧：我们可以通过二分法去逼近这个结果。因为我们的t值是[0,1]区间的,所以我们可以尝试二分解决，而二分法的精度是1/2^n,当n=10时，这个精度最大值便已经是1/1024≈0.001了，这对我们来说已经比较精确，但是还有方法可以将这个精度提升：
- 提高n的次数：n=20时这个精度值便为0.000001了，对于我们进行求值计算已经十分精确。
- 先控制区间，然后再在区间内进行二分逼近，比如先将t分成十份，然后将t对应的x值与目标值进行逐个比较，确定区间后进行二分操作，都可以。
除了二分法外，进行曲线上求值还有一个更为高效的方法，叫做牛顿迭代法，是根据曲线上某点坐标及其导数进行区间推导的过程，理解起来复杂程度较高，但是在适用条件内逼近精度平方级递增，效率奇高。想要更多了解相关知识的同学可以看一下我列的参考资料，或者还是求助万能的维基百科，我就不多做介绍了。
那没有具体介绍算法，咋写？这个比较好说，少年我送你一个库，这个库是我fork之后在主体文件上增加了注解。数学理论和计算机实践一个很大的不同就是：数学严谨且精确，而计算机计算则需要我们做更多权衡：精确度和性能，这个库很棒，能帮助我们理解算法同时也给出了生产解决方案，性能不俗。
那我们下一步就可以尝试使用这个解决方案来进行时间动画控制
制作自己的时间函数控制器
首先我们引入库，这个库导出的方法是bezier-curve，这个方法的调用返回值是一个函数，这个函数接受x作为参数，返回对应的y值，这个例子展示了这个功能，而以x为时间变量，y值的变化就是对应的运动函数，在这里我们使用t作为时间变化变量，tSpeed表示t变化快慢，然后通过requestAnimationFrame来不断进行渲染。
目前我们已经实现了一个小的三次贝塞尔曲线运动函数控制器，下一步我们需要解决的是什么呢？本篇文章未解决的问题，将有另一篇文章给出：
- 如何使用更为复杂的贝塞尔曲线来描述一个多节动画函数？
- 如何控制沿一般曲线运动物体的速度？
- 不借助SVG动画的帮助，我们如何实现物体沿一般复杂曲线运动并使运动物体自动旋转？
参考资料
https://www.geometrictools.com/Documentation/MovingAlongCurveSpecifiedSpeed.pdf
https://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/bezier-der.html
http://math.stackexchange.com/questions/12186/arc-length-of-b%C3%A9zier-curves
http://greweb.me/2012/02/bezier-curve-based-easing-functions-from-concept-to-implementation/
http://stackoverflow.com/questions/29438398/cheap-way-of-calculating-cubic-bezier-length
https://github.com/gre/bezier-easing/blob/master/src/index.js
