三个准则
1. 作为入门选手,不要每章都看
2. 不要从零造轮子去实现算法,太浪费时间
3. 必须能手推公式
章节目录
## 统计学习概论
- 统计学习的目的是对数据进行==预测与分析==
- 统计学习的前提是同类数据具有一定的统计规律性
- 统计学习的方法
- 监督学习(supervised learning)
- 非监督学习(unsupervised learning)
- 半监督学习(semi-supervised learning)
- 强化学习(reinforcement learning)
> 本书主要讨论监督学习
> 监督学习假设要学习的模型属于某个函数的集合
实现统计学习方法的步骤
- 得到一个有限的训练数据集合;
- 确定包含所有可能的模型的假设空间,即学习模型的集合;
- 确定模型选择的准则,即学习的策略;
- 实现求解最优模型的算法,即学习的算法;
- 通过学习方法选择最优模型;
- 利用学习的最优模型对新数据进行预测或分析;
统计学习研究一般包括三个方面
- 统计学习方法(statistical learning method)、
- 统计学习理论(statistical learning theory)
- 统计学习应用(application of statistical learning)
统计学习的应用
- 统计学习是处理海量数据的有效方法
- 统计学习是计算机智能化的有效手段
- 统计学习是计算机科学发展的一个重要组成部分
### 监督学习(supervised learning)
任务是学习一个模型,使模型能够对任意给定的输入,对其相应的输出做出一个好的预测
- 输入空间、输出空间
- 输入与输出所有可能取值的集合。
- 输入空间与输出空间可以是同一个空间,也可以是不同的空间;
- 但通常输出空间远远小于输入空间.
- 特征空间
- 每个具体的输入是一个实例(instance),通常由特征向量(feature vector)表示.
- 所有特征向量存在的空间称为特征空间(feature space)
预测任务的不同名称
- 输入变量与输出变量均为连续变量的预测问题称为==回归问题==;
- 输出变量为有限个离散变量的预测问题称为==分类问题==;
- 输入变量与输出变量均为变量序列的预测问题称为==标注问题==
联合概率分布
- 分布函数 (或分布密度函数):监督学习假设输入与输出的随机变量X 和Y遵循==联合概率分布==P(X,Y)
- 联合概率分布:是未知的、假定存在的
假设空间
- 输入到输出的映射 就是模型
- 学习目的是找出这个模型/映射
- 模型属于由输入空间 到输出空间的映射的集合
- 这个集合就是假设空间(hypothesis space)
- 假设空间的确定意味着学习范围的确定
模型可以是概率模型或非概率模型,可以用表示模型
- 概率分布 P(Y | X )
- 决策函数(decision function) Y = f ( X )
问题形式化
- 监督学习分为:==学习、预测== 两部分,对应训练和测试
### 统计学习方法的三要素
- 模型(model)
- $F = {f |Y = f(X)}$
- $F = {f |Y = f_c(X),}$参数c属于 $R^n$
- 策略(strategy)
- ==损失函数度量==:模型一次预测的好坏
对于给定的输入 X,通过 f ( X ) 给出相应的输出 与 真实值 的误差
损失函数值越小,模型就越好
- 0-1 损失函数
- 平方损失函数
- 绝对损失函数
- 对数损失函数
- ==风险函数度量==:平均意义下模型预测的好坏
学习的目标就是选择期望风险最小的模型
- 损失函数的期望:模型 f (X)关于联合分布P(X,Y)的平均意义下的损失,是不可计算的
- 经验风险:训练集的平均损失
- 样本容量 N 趋于无穷时,经验风 险 $R_{emp} ( f )$ 趋于期望风险 $R_{exp} ( f )$,但是训练集一般很小,要对经验风险进行一定的矫正。这就关系到监督学习的两 个基本策略: 经验风险最小化和结构风险最小化.
- 经验风险最小化 ERM
- 当样本容量足够大时,经验风险最小化能保证有很好的学习效果
- 极大似然估计是经验风险最小化的一个例子.当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化就等价于极大似然估计
- 当样本容量很小时,经验风险最小化可能出现过拟合现象
- 结构风险最小化 SRM
- 结构风险最小化等价于正则化
- 结构风险在经验风 险上加上表示模型复杂度的正则化项(regularizer)或罚项(penalty term)
- 贝叶斯估计中的最大后验概率估计MAP就是结构风险最小化的一个例子.当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化 就等价于最大后验概率估计
- 算法(algorithm)
- 学习模型的具体计算方法
### 模型评估与模型选择
训练误差:关于训练数据集的平均损失 $R_{emp}$
测试误差:测试数据集上的平均损失 $e_{test}$
测试数据集上的准确率:$r_{test}$
$r_{test} +e_{test}=1$ 见式1.18-1.21
模型选择:假设空间中存在“真”模型,我们选择的模型要尽量与真模型的数量一致
过拟合:如果一味追求提高对训练数据的预测能力,所选模型的复杂度则往往会比真模型更高。这种现象称为过拟合
- 过拟合对训练集数据预测的很好,但是对于未知数据预测的很差
- 选择模型时要提高模型的预测能力,同时也要避免过拟合
M次多项式: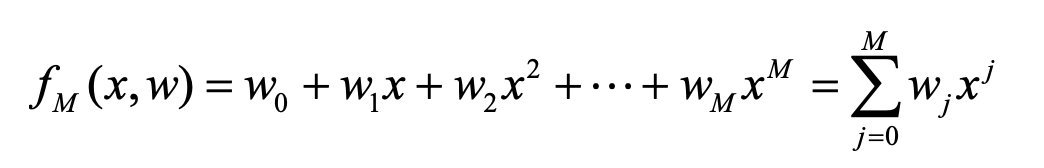
例1.1:训练集是十个点 $(x_i, y_i)$,假定给定数据符合M次多项式,选择最有可能的M次多项式
随着选择的模型越来越复杂,训练误差越小,但是预测误差会先减小,再增大(过拟合)
#### 正则化与交叉验证——模型选择方法
- 正则化是结构风险最小化策略的实现,是在经验风险上加一个==正则化项(regularizer)或罚项(penalty term)==
- 正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项(regularizer)或罚项(penalty term)
- 模型越复杂,正则化值就越大
- 见1.24式
- 正则化
#### 交叉验证——模型选择的方法
数据集充足时
随机的将数据集分为三部分:训练集用来训练模型,验证集用于模型的选择,而测试集用于最终对学习方法的评估
数据集不充足时可以采用交叉验证的方法选择模型
- 简单交叉验证
- 分成两部分:训练集、测试集。
- 用训练集在各种不同条件下得到不同模型,比较误差
- S-fold 交叉验证
- 分成大小相同的S个子集
- 用S - 1个作为训练,1个用于测试
- 这样有S种方法分割,重复S次,选出平均测试误差最小的模型
- 留一交叉验证
- 留一交叉验证是S-fold的特殊情形,当S = N时
### 泛化能力
泛化能力:指由该方法学习到的模型对未知数据的预测能力
### 生成模型与判别模型
### 分类问题
### 标注问题
### 回归问题
## 感知机
2.1感知机模型
2.2 感知机学习策略
2.2.1数据集的线性可分性
2.2.2 感知机学习策略
2.3 感知机学习算法
2.3.1 感知机学习算法的原始形式
2.3.2 算法的收敛性
2.3.3 感知机学习算法的对偶形式
## K近邻
可以不看
## 朴素贝叶斯
1朴素贝叶斯法的学习与分类
4.1.1基本方法
4.1.2后验概率最大化的含义
4.2 朴素贝叶斯法的参数估计
4.2.1极大似然估计
4.2.2 学习与分类算法
4.2.3 贝叶斯估计
## 决策树
5.1 决策树模型与学习
5.1.1 决策树模型
5.1.2 决策树与 if-then 规则
5.1.3 决策树与条件概率分布
5.1.4 决策树学习
5.2 特征选择
5.2.1 特征选择问题
5.2.2 信息增益
5.2.3 信息增益比
5.3 决策树的生成
5.3.1 ID3 算法
5.3.2 C4.5的生成算法
5.4 决策树的剪枝
5.5 CART 算法
5.5.1 CART生成
5.5.2 CART剪枝
## 逻辑回归和最大熵
6.1 逻辑斯谛回归模型
6.1.1 逻辑斯谛分布
6.1.2 二项逻辑斯谛回归模型
6.1.3模型参数估计
6.1.4 多项逻辑斯谛回归
6.2 最大熵模型
6.2.1 最大熵原理
6.2.2 最大熵模型的定义
6.2.3 最大熵模型的学习
6.2.4 极大似然估计
6.3 模型学习的最优化算法
6.3.1 改进的迭代尺度法
6.3.2 拟牛顿法
## 支持向量机
可以不看
## 提升树
8.1 提升方法 AdaBoost 算法
8.1.1 提升方法的基本思路
8.1.2 AdaBoost算法
8.1.3 AdaBoost的例子
8.2 AdaBoost 算法的训练误差分析
8.3 AdaBoost 算法的解释
8.3.1前向分步算法
8.3.2 前向分步算法与 AdaBoost
8.4提升树
8.4.1提升树模型
8.4.2提升树算法
8.4.3 梯度提升
## EM算法
可以不看
## 隐马尔科夫
可以不看
## 条件随机场
可以不看
## xgboost
必看
李航老师-统计学习
三个准则
1. 作为入门选手,不要每章都看
2. 不要从零造轮子去实现算法,太浪费时间
3. 必须能手推公式
章节目录
## 统计学习概论
- 统计学习的目的是对数据进行==预测与分析==
- 统计学习的前提是同类数据具有一定的统计规律性
- 统计学习的方法
- 监督学习(supervised learning)
- 非监督学习(unsupervised learning)
- 半监督学习(semi-supervised learning)
- 强化学习(reinforcement learning)
> 本书主要讨论监督学习
> 监督学习假设要学习的模型属于某个函数的集合
实现统计学习方法的步骤
- 得到一个有限的训练数据集合;
- 确定包含所有可能的模型的假设空间,即学习模型的集合;
- 确定模型选择的准则,即学习的策略;
- 实现求解最优模型的算法,即学习的算法;
- 通过学习方法选择最优模型;
- 利用学习的最优模型对新数据进行预测或分析;
统计学习研究一般包括三个方面
- 统计学习方法(statistical learning method)、
- 统计学习理论(statistical learning theory)
- 统计学习应用(application of statistical learning)
统计学习的应用
- 统计学习是处理海量数据的有效方法
- 统计学习是计算机智能化的有效手段
- 统计学习是计算机科学发展的一个重要组成部分
### 监督学习(supervised learning)
任务是学习一个模型,使模型能够对任意给定的输入,对其相应的输出做出一个好的预测
- 输入空间、输出空间
- 输入与输出所有可能取值的集合。
- 输入空间与输出空间可以是同一个空间,也可以是不同的空间;
- 但通常输出空间远远小于输入空间.
- 特征空间
- 每个具体的输入是一个实例(instance),通常由特征向量(feature vector)表示.
- 所有特征向量存在的空间称为特征空间(feature space)
预测任务的不同名称
- 输入变量与输出变量均为连续变量的预测问题称为==回归问题==;
- 输出变量为有限个离散变量的预测问题称为==分类问题==;
- 输入变量与输出变量均为变量序列的预测问题称为==标注问题==
联合概率分布
- 分布函数 (或分布密度函数):监督学习假设输入与输出的随机变量X 和Y遵循==联合概率分布==P(X,Y)
- 联合概率分布:是未知的、假定存在的
假设空间
- 输入到输出的映射 就是模型
- 学习目的是找出这个模型/映射
- 模型属于由输入空间 到输出空间的映射的集合
- 这个集合就是假设空间(hypothesis space)
- 假设空间的确定意味着学习范围的确定
模型可以是概率模型或非概率模型,可以用表示模型
- 概率分布 P(Y | X )
- 决策函数(decision function) Y = f ( X )
问题形式化
- 监督学习分为:==学习、预测== 两部分,对应训练和测试
### 统计学习方法的三要素
- 模型(model)
- $F = {f |Y = f(X)}$
- $F = {f |Y = f_c(X),}$参数c属于 $R^n$
- 策略(strategy)
- ==损失函数度量==:模型一次预测的好坏
对于给定的输入 X,通过 f ( X ) 给出相应的输出 与 真实值 的误差
损失函数值越小,模型就越好
- 0-1 损失函数
- 平方损失函数
- 绝对损失函数
- 对数损失函数
- ==风险函数度量==:平均意义下模型预测的好坏
学习的目标就是选择期望风险最小的模型
- 损失函数的期望:模型 f (X)关于联合分布P(X,Y)的平均意义下的损失,是不可计算的
- 经验风险:训练集的平均损失
- 样本容量 N 趋于无穷时,经验风 险 $R_{emp} ( f )$ 趋于期望风险 $R_{exp} ( f )$,但是训练集一般很小,要对经验风险进行一定的矫正。这就关系到监督学习的两 个基本策略: 经验风险最小化和结构风险最小化.
- 经验风险最小化 ERM
- 当样本容量足够大时,经验风险最小化能保证有很好的学习效果
- 极大似然估计是经验风险最小化的一个例子.当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化就等价于极大似然估计
- 当样本容量很小时,经验风险最小化可能出现过拟合现象
- 结构风险最小化 SRM
- 结构风险最小化等价于正则化
- 结构风险在经验风 险上加上表示模型复杂度的正则化项(regularizer)或罚项(penalty term)
- 贝叶斯估计中的最大后验概率估计MAP就是结构风险最小化的一个例子.当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化 就等价于最大后验概率估计
- 算法(algorithm)
- 学习模型的具体计算方法
### 模型评估与模型选择
训练误差:关于训练数据集的平均损失 $R_{emp}$
测试误差:测试数据集上的平均损失 $e_{test}$
测试数据集上的准确率:$r_{test}$
$r_{test} +e_{test}=1$ 见式1.18-1.21
模型选择:假设空间中存在“真”模型,我们选择的模型要尽量与真模型的数量一致
过拟合:如果一味追求提高对训练数据的预测能力,所选模型的复杂度则往往会比真模型更高。这种现象称为过拟合
- 过拟合对训练集数据预测的很好,但是对于未知数据预测的很差
- 选择模型时要提高模型的预测能力,同时也要避免过拟合
M次多项式: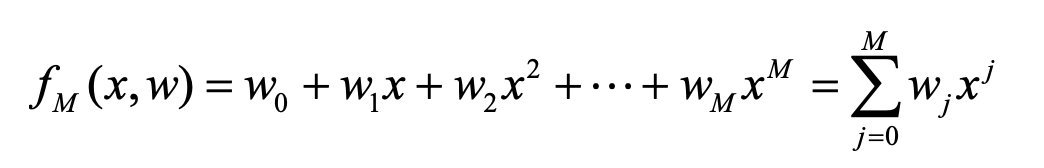
例1.1:训练集是十个点 $(x_i, y_i)$,假定给定数据符合M次多项式,选择最有可能的M次多项式
随着选择的模型越来越复杂,训练误差越小,但是预测误差会先减小,再增大(过拟合)
#### 正则化与交叉验证——模型选择方法
- 正则化是结构风险最小化策略的实现,是在经验风险上加一个==正则化项(regularizer)或罚项(penalty term)==
- 正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项(regularizer)或罚项(penalty term)
- 模型越复杂,正则化值就越大
- 见1.24式
- 正则化
#### 交叉验证——模型选择的方法
数据集充足时
随机的将数据集分为三部分:训练集用来训练模型,验证集用于模型的选择,而测试集用于最终对学习方法的评估
数据集不充足时可以采用交叉验证的方法选择模型
- 简单交叉验证
- 分成两部分:训练集、测试集。
- 用训练集在各种不同条件下得到不同模型,比较误差
- S-fold 交叉验证
- 分成大小相同的S个子集
- 用S - 1个作为训练,1个用于测试
- 这样有S种方法分割,重复S次,选出平均测试误差最小的模型
- 留一交叉验证
- 留一交叉验证是S-fold的特殊情形,当S = N时
### 泛化能力
泛化能力:指由该方法学习到的模型对未知数据的预测能力
### 生成模型与判别模型
### 分类问题
### 标注问题
### 回归问题
## 感知机
2.1感知机模型
2.2 感知机学习策略
2.2.1数据集的线性可分性
2.2.2 感知机学习策略
2.3 感知机学习算法
2.3.1 感知机学习算法的原始形式
2.3.2 算法的收敛性
2.3.3 感知机学习算法的对偶形式
## K近邻
可以不看
## 朴素贝叶斯
1朴素贝叶斯法的学习与分类
4.1.1基本方法
4.1.2后验概率最大化的含义
4.2 朴素贝叶斯法的参数估计
4.2.1极大似然估计
4.2.2 学习与分类算法
4.2.3 贝叶斯估计
## 决策树
5.1 决策树模型与学习
5.1.1 决策树模型
5.1.2 决策树与 if-then 规则
5.1.3 决策树与条件概率分布
5.1.4 决策树学习
5.2 特征选择
5.2.1 特征选择问题
5.2.2 信息增益
5.2.3 信息增益比
5.3 决策树的生成
5.3.1 ID3 算法
5.3.2 C4.5的生成算法
5.4 决策树的剪枝
5.5 CART 算法
5.5.1 CART生成
5.5.2 CART剪枝
## 逻辑回归和最大熵
6.1 逻辑斯谛回归模型
6.1.1 逻辑斯谛分布
6.1.2 二项逻辑斯谛回归模型
6.1.3模型参数估计
6.1.4 多项逻辑斯谛回归
6.2 最大熵模型
6.2.1 最大熵原理
6.2.2 最大熵模型的定义
6.2.3 最大熵模型的学习
6.2.4 极大似然估计
6.3 模型学习的最优化算法
6.3.1 改进的迭代尺度法
6.3.2 拟牛顿法
## 支持向量机
可以不看
## 提升树
8.1 提升方法 AdaBoost 算法
8.1.1 提升方法的基本思路
8.1.2 AdaBoost算法
8.1.3 AdaBoost的例子
8.2 AdaBoost 算法的训练误差分析
8.3 AdaBoost 算法的解释
8.3.1前向分步算法
8.3.2 前向分步算法与 AdaBoost
8.4提升树
8.4.1提升树模型
8.4.2提升树算法
8.4.3 梯度提升
## EM算法
可以不看
## 隐马尔科夫
可以不看
## 条件随机场
可以不看
## xgboost
必看