Given n non-negative integers a1, a2, ..., an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container.
给定n个非负的整数a1, a2, ..., an,(i, ai) and (i, 0)分别代表坐标(i, ai)。连接(i, ai) and (i, 0)画直线,共有n条。找出两条直线,使得两条直线与x轴形成的容器能够盛最多的水。
分析
如果容器盛水最多
- 矩形面积最大。
- 盛水量的多少,由两条垂线中较短的一条决定。
- 两条垂线中较短一条尽可能长。
算法解析
如图所示
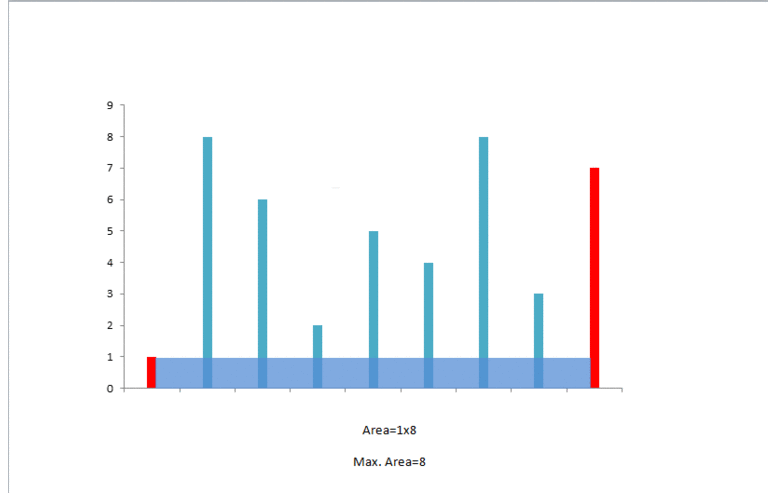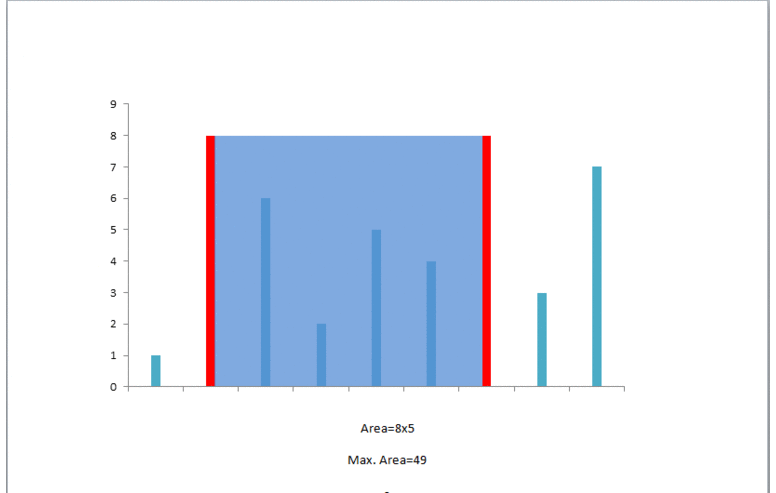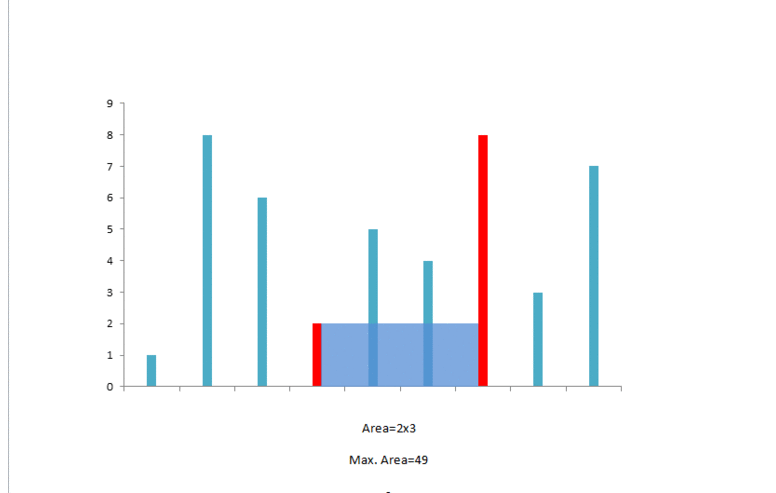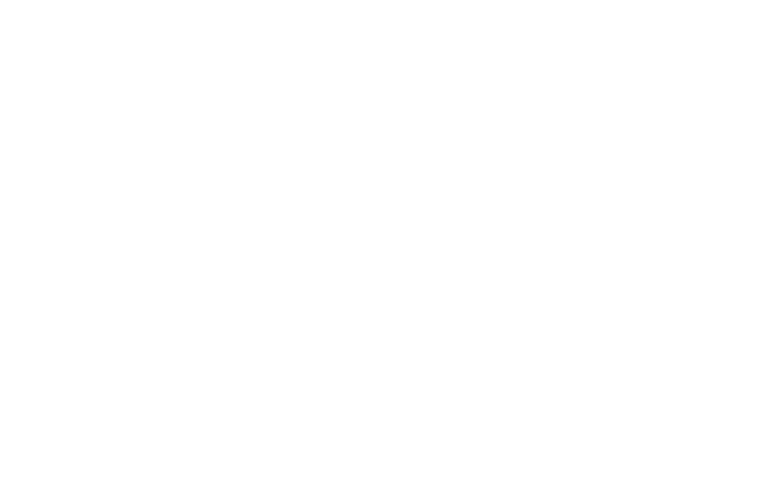
算法解析
以序列最外面两条边形成的面基为起始面积,找出两条边中较小的一条,索引加一(i++),原因是找出一条更大的边来代替较小的边,以使得整个容器最大。
答案
public class Solution {
public int maxArea(int[] height) {
int maxArea = 0, left = 0;
int right = height.length - 1;
while (left < right) {
maxArea = Math.max(maxArea, Math.min(height[left], height[right]) * (right - left));//求两点之间的面积
if (height[left] < height[right]) {
left ++;
} else {
right--;
}
}
return maxArea;
}
}