数据预处理
数据清洗
- 离散化
对于在连续性随机变量上计算信息熵,需要将变量离散化。其概率密度函数f(x)的定义为:
2}{2\sigma^2})
其中:
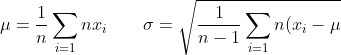 ^2})
这里f(x)的是概率密度并不是相关概率,所以其值可能>1,详情请查阅任意一本概率统计书籍。 - 特征缩放
当样本中的数据的度量单位不一致的时候,使用这些距离度量公式的时候有一个非常大的弊端,就是量纲较大的属性产生的影响会显得比较大很肯能掩盖掉了一些很重要的属性的影响,为此我们需要对数据进行标准化。使他们处于同一个水平进行比较和度量。对于标准化后的数据进行训练,不能对新来的未知数据的预测有较好的鲁棒性。下图是标准化转换计算公式-
1.min-max标准化(Min-Max Normalization)
也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 - 1]之间。转换函数如下:
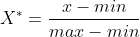
其中max为样本数据的最大值,min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。 -
2. Z-score标准化方法
这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,转化函数为:
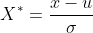
-
1.min-max标准化(Min-Max Normalization)
- 离散特征数值化
- 有序特征
如果特征之间存在序的关系,需要手动转化为数值型数据。例如大>中>小-->[2,1,0] - 无序特征
程序猿,产品经理,测试人员,公司老总这类不存在顺序的情况,转换为[0001],[0100],[0010],[1000]
sklearn中不支持离散数值,所有的离散型随机变量都需要转换成数值型,具体转换规则以上已经给出
- 有序特征
特征选择
- 随机森林
- 互信息
- 卡方检验
- 方差检验
- 相关系数
- 递归特征消法
- SBS特征选择算法
维度处理
- PCA主成分分析
- SVD奇异值分解
- L1 正则化
- 线性判别分析(LDA)
- 词频逆文档(tf-idf)
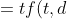 \bullet idf(t,f))
 = log{\frac{n_d}{1+df(t,d)}})
度量指标
欧几里得距离
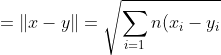2})余弦相似度
= \frac{ A \bullet B}{\Vert A \Vert \Vert B \Vert}=\frac{\displaystyle \sum_{i=1}^nA_i \times B_i}{\sqrt{\displaystyle \sum_{i=1}n(A_i)2 \times \displaystyle \sum_{i=1}n(B_i)2}})Jaccard距离或相似度Mahalanobis距离Hamming距离(汉明距离)Manhattan距离(曼哈顿距离)闵可夫斯基距离(MinkowskiDistance)
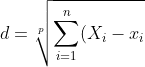^p})
当$p$为1的时候就是曼哈顿距离,为2的时候就是欧氏距离。
分类评估
混淆矩阵用来描述正确分类和错误分类的各个指标。下面是一个二分类问题混淆矩阵的实例。

- 准确率 :
- 正确率 :
- Negative Predictive Value :
- 敏感度:
- 特异性:
ROC曲线
回归评估
Mean Squared Error(均方误差)
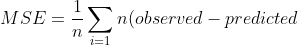2)
Root Mean Squared Error(均方根误差)
均方差用来衡量回归模型中的错误率,注意不同模型计算时需要注意度量单位的统一。
2}{n}})
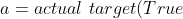 \qquad p=predicted \ target(predicted))
Relative Squared Error(相对误差平方)
2}{\displaystyle \sum_{i=1}^n(\overline a-a_i)^2})
Mean Absolute Error(平均绝对误差)
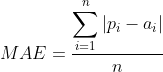
Relative Absolute Error(相对绝对误差)
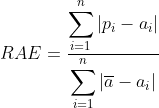
优化方法
-
最小二乘法
最小二乘法就是就求均方差最小。
 = argmin(RMSE))
梯度上升(下降)寻求最大(最小)值
梯度上升法基于的思想是:要找到函数的最值最好的方法就是沿着函数的地图方向进行。从初始点进行最值寻找的过程中需要计算当期点的梯度,并且沿着这个方向移动,具体移动的步伐通过步长来设定。到达下一个点之后重新计算梯度不迭代直到满足条件。(寻找到最优值或者到达误差允许的范围内。)
ps:梯度下降个人理解为求微分寻找全局最小值,使得函数的代价最小。随机梯度
随机梯度在针对大数据集的时候显得特别有用,虽然损失了一定的精度,但是换来了较快的收敛速度,达到一个与全局最优较近位置的点。它是针对每个点选择盖点最优的方向进行移动,不一定要对整个数据集集合操作就可能到达收敛了。而BGD(批处理梯度下降)在每一次梯度的更新操作中需要对整个数据集进行计算,在大数据处理过程中无疑增大了计算量。最大似然估计
风刮的L1 与 L2 正则化
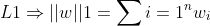
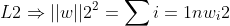
其他
多分类问题
最经典的拆分策略有三种:
“一对一”(
One vs. One,OvO)“一对其余”(
One vs. Rest,OvR)-
“多对多”(
Many vs. Many,MvM)给定数据集 $D={(x_1,y_1),(x_2,y_2),...(x_n,y_n)} \quad y_i \in{C_1,C_2,...C_n}$,OvO将这两个类别两两配对,从而产生
N(N-1)/2个分类任务

类别不平衡问题
- 欠采样
- 过采样
- 阀值移动
常用算法(模型的建立)
分类
分类问题实际是一类监督学习问题,根据训练数据的类标记来引导分类器选择合适的参数,较好的拟合样本空间中的数据,并且能够对未来的数据有一定的预测能力(泛化能力)。分类算法大致可以按照如下四种方式进行分类。
ZeroR
Weka中提供了ZeroR算法,是最简单的分类器。主要思想是按照类中大多数数据所属的类别类进行分类。基本上没有使用认为关于ml的理论。它的作用就是给其他分类器提供一个模型的基线,衡量一个算法的性能。换句话说我们用的模型再怎么不行也不能比这个baseline还要低吧。
构造目标的频率表,选择频率最大的类别作为目标的预测值

下面是ZeroR的混淆矩阵,我们可以看到这个算法的用途只是在于提供一个baseline而已。

OneR
OneR是“One Rule”的简称,也就是按照一个规则进行分类。它会针对每个属性上进行测试对目标进行分类,然后从每个属性中得到的规则中选择最小误分类的规则作为最终的分类模型。比如下面的例子很好的说明上述的描述。
一个较小的总体分类误差意味着对正确分类提供了更多的贡献。

这是这个分类问题的混淆矩阵

朴素贝叶斯(Naive Bayesian)
贝叶斯分类依托于贝叶斯理论。基于先验概率的理解,根据样本数据的统计特征得出后验概率。是一种非常简单而且有效的分类方法。在数据较少的情况下也依然有效,同时也可以处理多类分类问题。缺点在于对输入数据的准备方式较为敏感。
补充贝叶斯公式、贝叶斯理论
to be continue... 、
朴素贝叶斯的前提条件是:假设给定目标值时属性之间彼此相互独立。然后应用贝叶斯公式通过 $P(c) ,P(x) ,P(x/c)$ 计算出后验概率$P(c/x)$。虽然我们不能确定给定的属性之间是否真的相互独立,但是在这么一个假设的前提下,朴素贝叶斯分类确实取得了非常不错的效果。

下面举个栗子,看看贝叶斯的分类机制。
给定一个属性集合计算它属于其中某个类别的一个后验概率,然后选择概率最大的那个类别作为它的分类。需要注意的一点就是由于贝叶斯针对多个变量的连乘操作,我们在操作中需要进行加一避免0的出现。比如途中当outlook为overcast的时候(Play Golf=no)。

- 正态分布

连续性数值求概率:
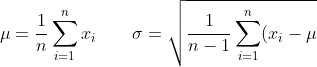^2} \qquad f(x) = \frac{1}{\sqrt{2\pi}\sigma}e\frac{-(x-\mu)2}{2\sigma^2})
$f(x)$ 称为概率密度
决策树 (Decision Tree)
决策树可用来构建分类和回归模型,能够处理离散型和连续型的数据。分类的过程就是不断的把数据集合按照属性分成一个个较小的子集,属性的选择可用比如信息增益等方式,对每个选择的属性做一次判断然后将数据归入到特定的子集中不断的进行直到分类完全。这个用来做分析判断的属性所在的节点叫做决策节点也是最终形成树的中间节点。最后形成的树的叶子节点表示纯类。

构造决策树的核心算法来自 J.R.Quinlan发表的ID3算法,ID3使用的是自顶向下的贪婪算法,不经过回退操作在整个可能的空间中进行搜索.ID3使用熵和信息增益来构建决策树。
- 熵
ID3使用熵(平均信息量)来计算样本间的同质性。即如果样本完全同质则信息熵为0,如果样本均匀包含各种可能性,则熵为1.熵在某种程度上表达了不确定性的多少。不确定性越大信息熵越大。数学之美一书中阐述过香农的信息熵理论。

使用id3进行构建决策树时候,需要计算两类熵。
- 单个属性的信息熵

- 多个属性的信息熵

- CART(基尼指数)
- C4.5(信息增益,ID3的改进算法)
信息增益是基于在针对数据集上一个属性上分类之后熵的减少来定义的。构造决策树的过程实际上就是不断的寻找分裂属性并且返回最大的信息增益值,这意味着分裂后的分支所在的集合信息熵越小,它所在的分支越纯,从而达到了分类的效果。下面是计算步骤1-5。
1.计算分类目标的的熵
2.将数据集按照不同的属性划分并且计算他们分裂之后的熵和信息增益。ent_three.png
3.选择最大的信息增益作为决策节点。这里选择的是outlook.
4.当摸个分支的熵为0的时候则表示已经分类完成,直接作为叶子节点。否则的话继续选择属性进行分裂。
5.递归的运行ID3算法直到数据集被完全划分而且没有决策节点。
线性判别分析
线性判别分析被R. A. Fisher在1936年首次作为一种分类方法提出,具有与复杂方法相当的精确度。
LDA基于这样一种思想,就是在预测变量的线性组合空间中搜索最佳的用来分开两个类(target)的线性组合。Finsher定义了下面的 *代价函数 *。
逻辑回归
逻辑回归产生一条逻辑曲线将值映射到[0,1]之间,逻辑回归于线性回归有点类似,不过这条曲线使用的是目标变量的可能性的自然对数而不是概率来构造。而且预测变量不必满足正态分布或在同一个组内要求的相同方差。 逻辑回归不仅可以处理数值型数据而且可以处理分类型变量.
逻辑回归使用sigmoid函数作为回归分类器,我们通过在每个特征上乘以一个回归系数,然后把所有的结果相加得到一个总和带入到sigmoid这个阶跃函数中,进而得到一个0~1之间的实数,我们把大于0.5的归入到1类,小于0.5的归入到0类。所以逻辑回归也可以被看成是一个概率估计分类器。
那么最佳的回归系数怎么确定呢?这就需要采用最优化的方法来进行对参数的确定了,拟合训练数据学习出最佳的回归系数就是逻辑回归训练的任务了。
K最邻算法(K Nearest Neighbors)
K近邻是比较简答基于相似度来分类的一个算法,核心思想就是根据距离来寻找与待分类点的k个邻居,然后每个对应邻居节点都有自己的类标号,我们选择这k个邻居中类标号数目最多的作为待分类节点的标签,类似于一种投票机制。k近邻是一种lazy算法。处理待分类节点的时候才去寻找他对应的邻居。
- K的选择
一般选择k的范围为[3,10]当然只是个别的经验,通过交叉验证的方式可以帮助我们选择合适的k值并通过独立的验证集来验证这个k是否合适,这对分类器的分类效果至关重要。
感知机
神经网络(Artificial Neural Network)
人工神经网络是基于生物神经网络的一个系统。模仿大脑内的神经元之间的触发方式。到达临界条件才会激活或者抑制。人工神经网络(ANN)由三个部分组成:输入层、隐含层、输出层。

传递方式 : 1.前向传播 ,2.后向反馈


