机器学习更多内容可以关注github项目:machine learning
数据的输入质量决定了输出的最后结果,数据的探索、预处理、特征选择、降维等特征工程占了项目的70%的时间。那么如果我们确定了商业目的,该如何一步一步渐进式进行特征工程呢?各位看官不急,请小的慢慢给你道来。
我前面有几遍文章也是介绍特征工程,但大致介绍特征工程包含哪些内容,知识比较离散化,如果在一个实际项目中,什么时候使用什么方法,没有贯穿起来。在看此篇文章时,大家可以对照看。
在建立模型前,我们大致需要顺序经过以下几步:
1、变量识别
2、单变量分析
3、双变量分析
4、缺失值处理
5、异常值处理
6、变量变化
7、变量创建
4-7在模型优化中会重复进行。
变量识别
首先,识别Predictor(即feature、输入)和Target(输出)变量。 接下来,确定变量的数据类型和类别。
举一个例子,让我们更清楚地了解这一步。 假设我们想预测学生是否会玩板球(参考下面的数据集),需要识别预测变量、目标变量,变量的数据类型和变量类别。
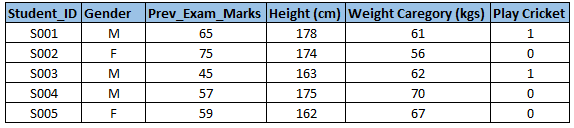
那么

单变量分析(Univariate Analysis)
在这个阶段,我们逐个探索变量。 执行单变量分析的方法取决于变量类型是分类类型还是连续类型。
连续变量(Continuous Variables)
在连续变量的情况下,我们需要了解变量的中心趋势和分散,使用各种统计度量可视化方法进行测量,如下所示

分类变量(Categorical Variables)
对于分类变量,我们可使用频率表来了解每个类别的分布,也可以读取每个类别下的值的百分比,也可以使用每个类别的Count和Count%来衡量。Bar chart可以用作可视化。
双变量分析
双变量分析的主要目的是发现两个变量之间的关系。可以对分类和连续变量的任何组合执行双变量分析。如:Continuous & Continuous,Categorical & Categorical,Categorical & Continuous and Continuous & Continuous。
Continuous & Continuous
在两个连续变量之间进行双变量分析时,散点图( scatter plot)是找出两个变量之间的关系的一个很好的方式。 散点图表示变量之间的关系可以是线性或非线性。

- -1: perfect negative linear correlation
- +1:perfect positive linear correlation and
- 0: No correlation
scatter plot只是直观来看,但是相关性如何计算呢?一般通过Pearson Correlation 来计算,缺点是:只可以确定线性相关性。非线性关系,可以采用互信息法,互信息系数能够很好地度量各种相关性,但是计算相对复杂一些。Pearson Correlation 计算方法如下:

Step 1: 计算x、y的均值
Step 2: x的每个值减去x的均值得到a, y值做类似操作得到b
Step 3: 计算: a × b, a的平方和b的平方
Step 4: 求a × b, a平方和b平方的和
Step 5: 如5的公式
Categorical & Categorical
双向表:我们可以通过创建一个计数和计数%的双向表来开始分析关系,行表示一个变量的类别,列表示另一个变量的类别,如图。

Stacked Column Chart:更直观,如上图。
卡方检验:计算方法可以参考前面文章
确定自变量和因变量的相关性
p值为0:表示两个变量是相关的
p值为1:表示两个变量是独立的
Categorical & Continuous
在探索分类和连续变量之间的关系时,我们可以为每个级别的分类变量绘制box plot,但不显示统计学意义。 为了看统计学意义,我们可以进行Z检验,T检验或方差分析。
T检验与Z检验非常相似,但用于当两个类别的观察次数小于30时,方差分析用于评估两个以上组的平均值是否在统计学上不同。
下篇再接着介绍。
参考
central measures
range
https://www.analyticsvidhya.com/blog/2016/01/guide-data-exploration/