强连通分量
相关概念
强连通:在有向图G中,如果两个顶点u,v间存在一条u到v的路径且也存在 一条v到u的路径,则称这两个顶点u,v是强连通的。
强连通图:如果有向图G的任意两个顶点都强连通,则称G是一个强连通图。
强连通分量:有向非强连通图的极大强连通子图,称为强连通分量。(极大强连通子图:G是一个极大强连通子图,当且仅当G是一个强连通子图且不存在另一个强连通子图G’,使得G是G’的真子集。)
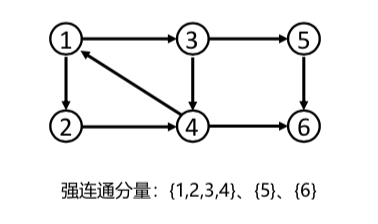
示意图
强连通分量题目的求解
kosaraju算法
基于两次DFS的有向图强联通子图算法。
1.对原有向图G进行DFS,记录结点访问完的顺序d[i],d[i]表示第i个访问完 的结点是d[i];
2.选择具有最晚访问完的顶点,对反向图GT进行DFS,删除能够遍历到的 顶点,这些顶点构成一个强联通分量;
3.如果还有顶点没有删除,继续第2步,否则算法结束。
代码实现
void dfsOne(int x) //对原图G搜索
{
vst[x]=1;
for(int i=1;i<=n;i++)
if(! vst[i] && map[x][i]) dfsOne(i)//此处map是用的邻接矩阵存边,当然链式前向星也可以,而且效率更高
d[++t]=x;//d数组见算法介绍
}
void dfsTwo(int x) //对逆图GT搜索
{
vst[x]=t;//vst记录到没到过
for(int i=1;i<=n;i++)
if(! vst[i] && map[i][x]) dfsTwo(i)
}
void Kosaraju()
{
int i,t=0;
for(i=1;i<=n;i++)
if(! Vst[i]) dfsOne(i);
memset(vst,0,sizeof(vst));
t=0;
for(i=n;i>=1;i--)
if(! vst[d[i]]){
t++;
dfsTwo(d[i]);
}
}
推荐一道题,是一道裸的kosaraju:迷宫城堡
思路:其实这题就是在问整个图是不是一个强连通图。
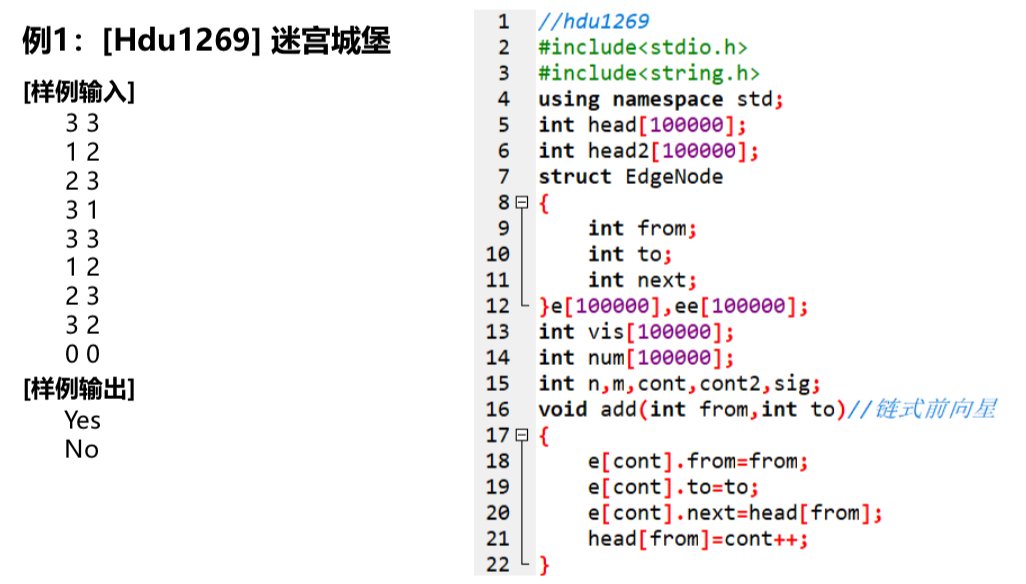
题目
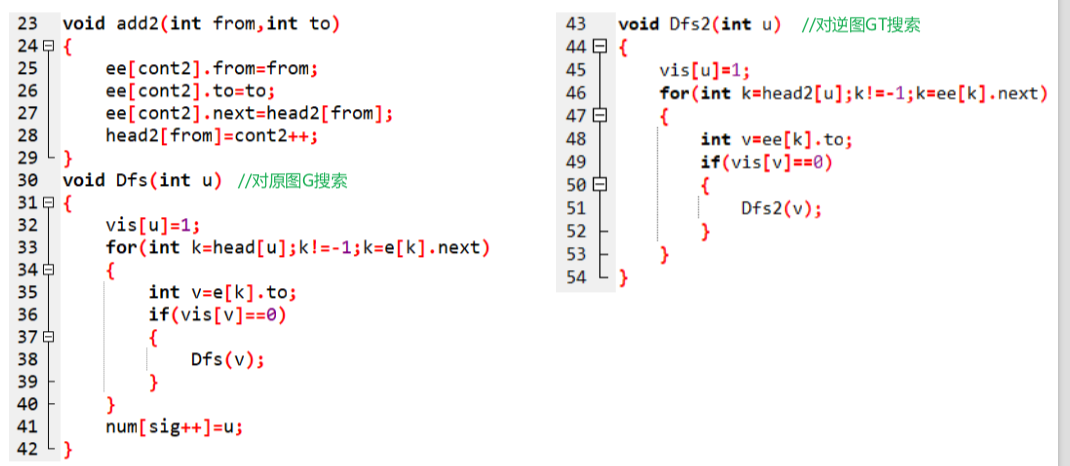
例题
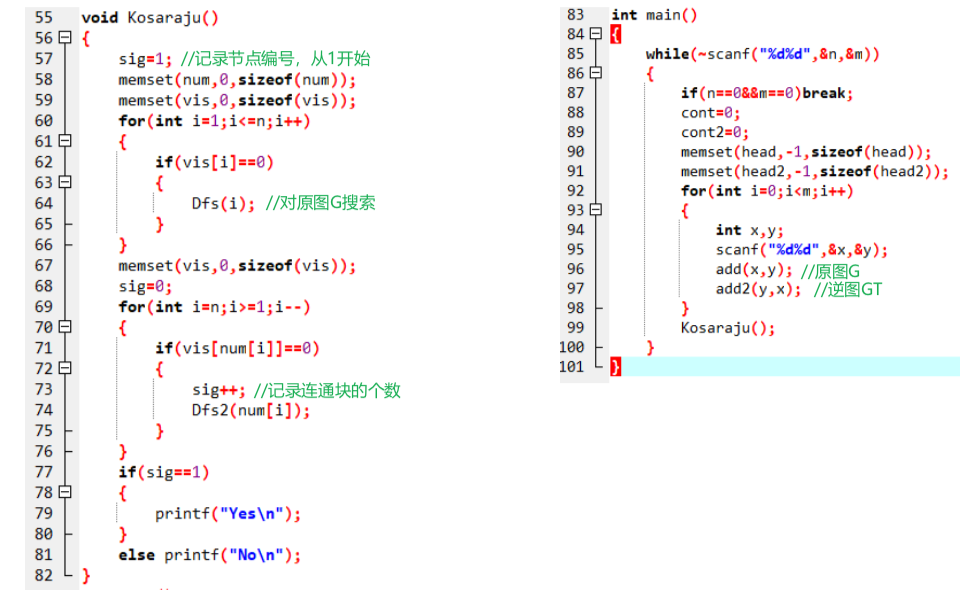
例题
tarjan(太监)?
Tarjan算法是基于有向图深度优先搜索的算法。每个强连通分量为搜索树中 的一颗子树。搜索时,把当前搜索树中未处理的结点加入一个栈,回溯时可以判 断栈顶到栈中的结点是否构成一个强连通分量。
定义:
DFN[u]为结点u的搜索次序编号(时间戳) Low[u]为u或u的子树能够回溯到的最早的栈中结点的DFN值。

tarjan
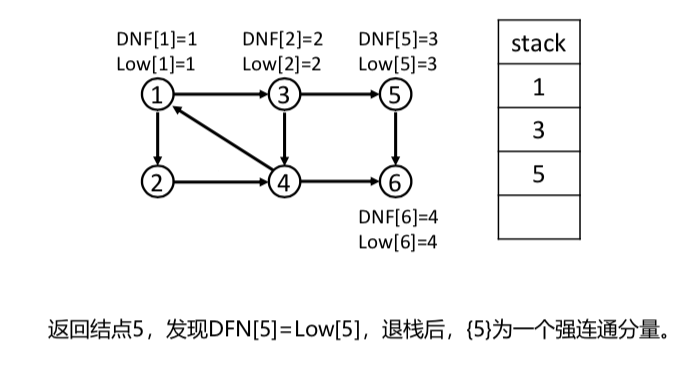
tarjan
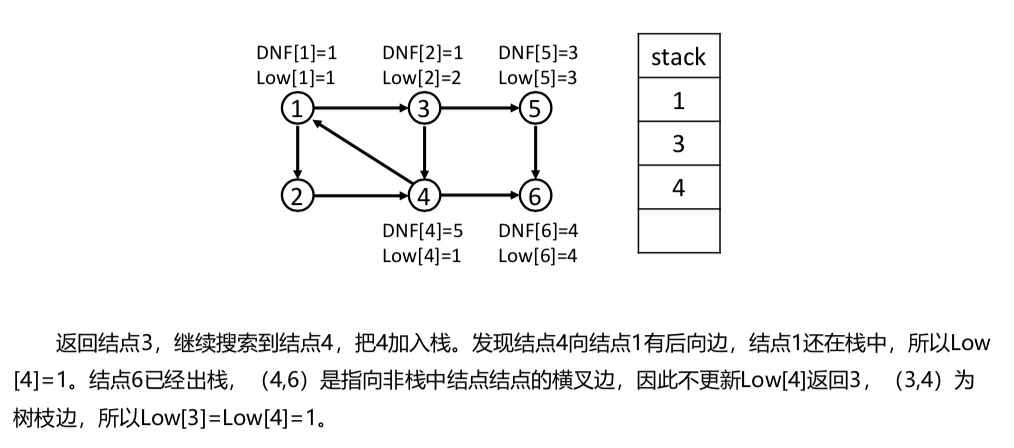
tarjan
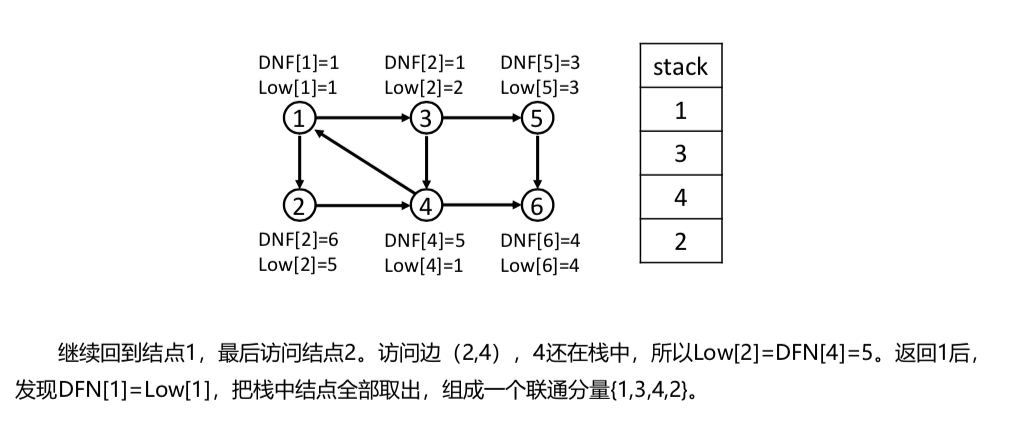
tarjan
这有一个tarjan模版

tarjan
说一下缩点,意思就是把一个强连通分量就记为一个点,这样下来图的点数可以减少。
结尾
强连通分量经常用来处理点与点的关系,在提高组及以上会出现。可以拿来处理一些团体与团体之间的题。
下面给出一些例题

problem