# 图计算
# 图的基础知识
## 什么是图
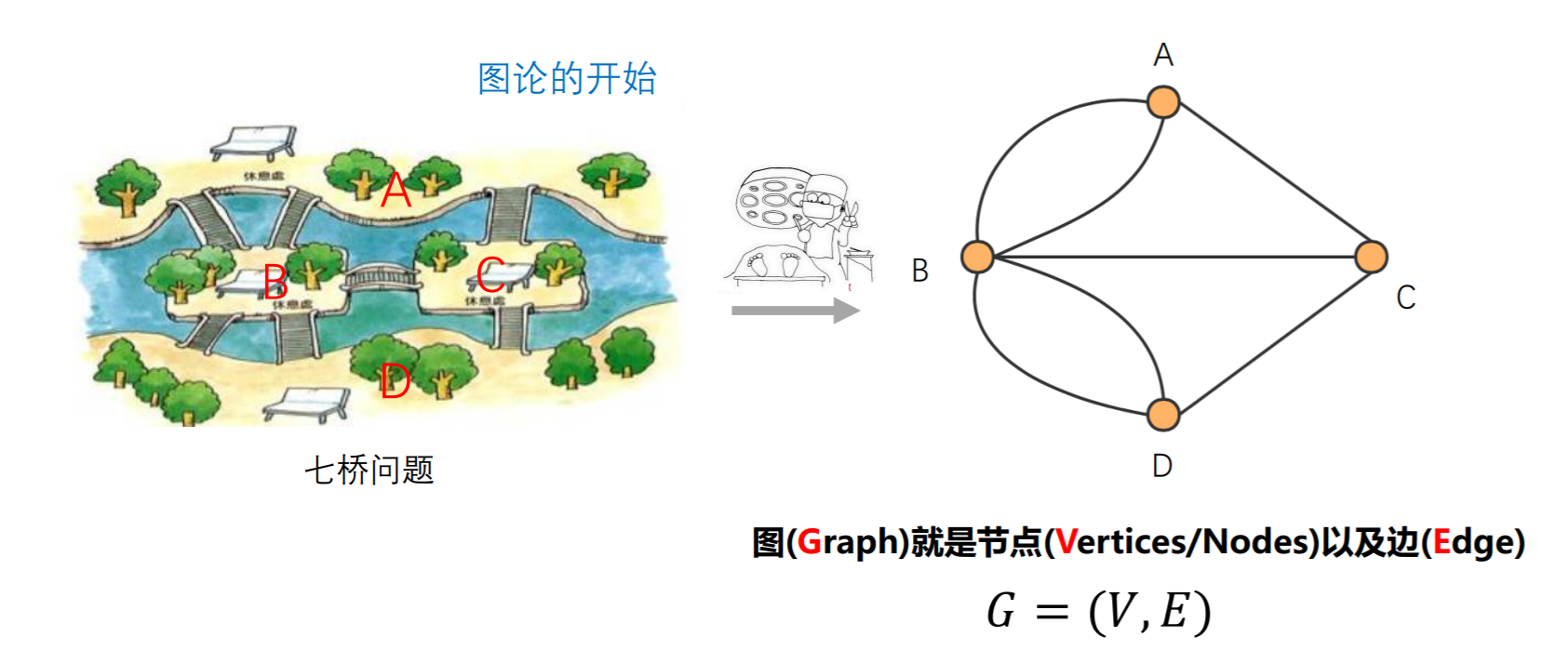
## 图的分类
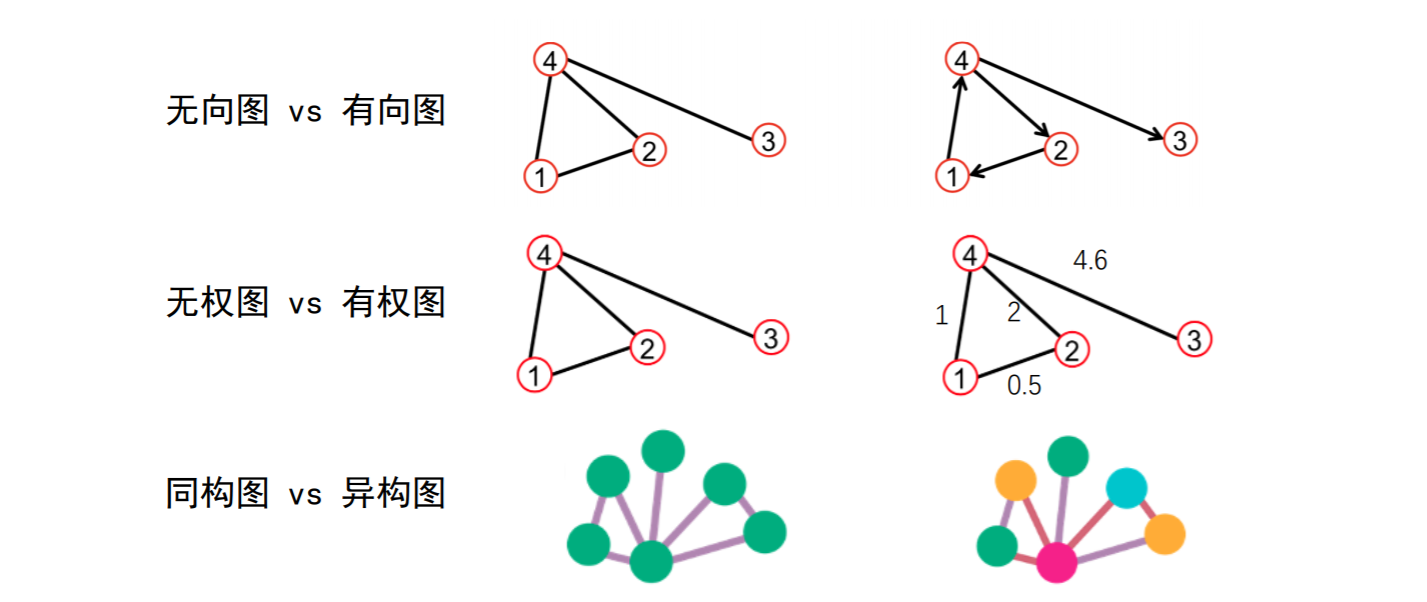
- 有向图:有指示方向
- 有权图:每条边有各自的权重
- **同构图**(Homogeneous Graph)数据中只存在一种节点和边,因此在构建神经网络时所有节点共享同样的模型参数并且拥有同样维度的特征空间。
- **异构图**(Heterogeneous Graph)中可以存在不只一种节点和边,因此允许不同类型的节点拥有不同维度的特征或属性。
## 同构图和异构图的差异
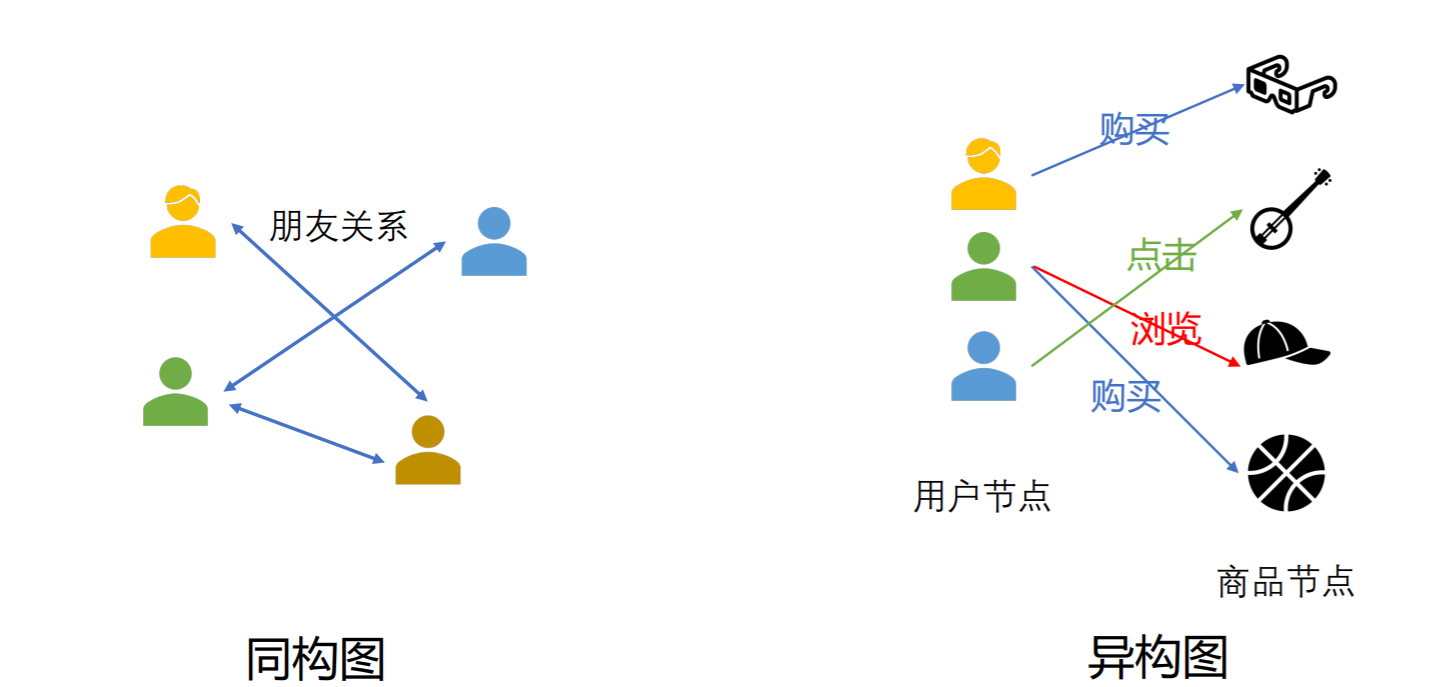
- 同构图只存在一种行为/关系
- 异构图存在多种行为/关系
## 度和邻居
### 度
一个顶点的度(degree)指与该顶点关联的边的数目。当边有权重时,就是所有边的权重和。记做deg(v)deg(v)。
在有向图中,还有出度(out-degree)和入度(in-degree)的概念。
出度(out-degree)指以该顶点为起点的边的权重和,入度(in-degree)指的是以该顶点为终点的边的权重和。

## 邻接矩阵
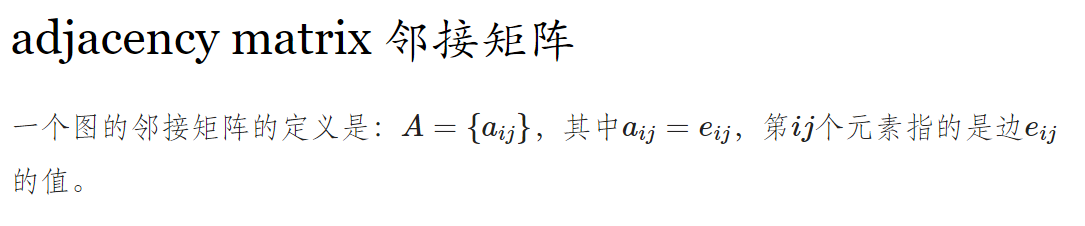
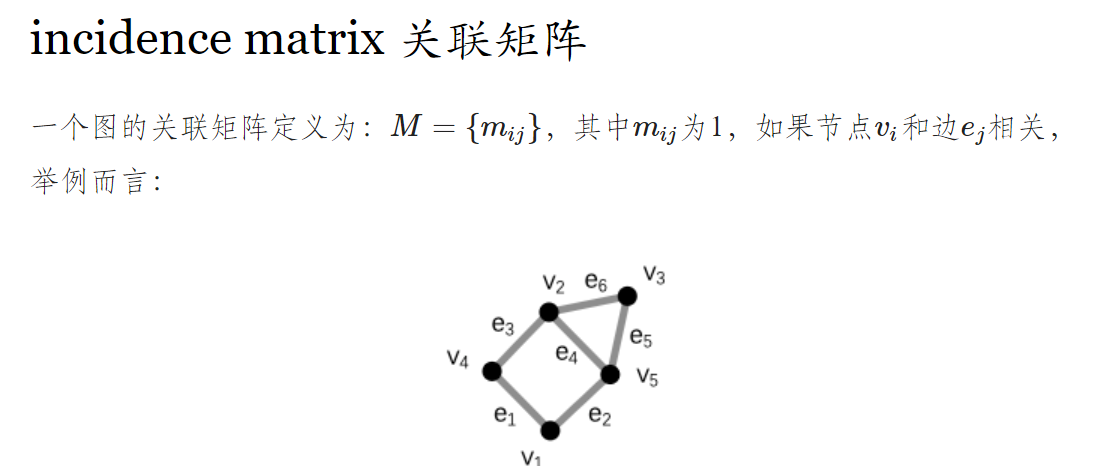
对应的关联矩阵
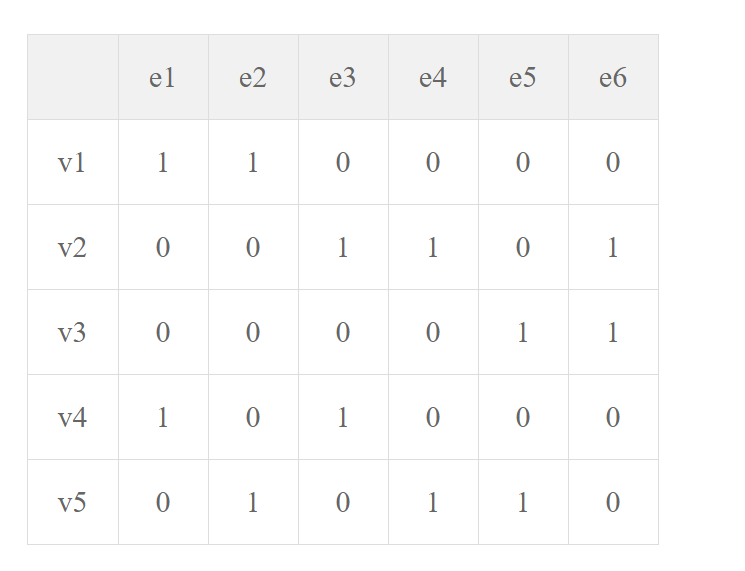
举例:
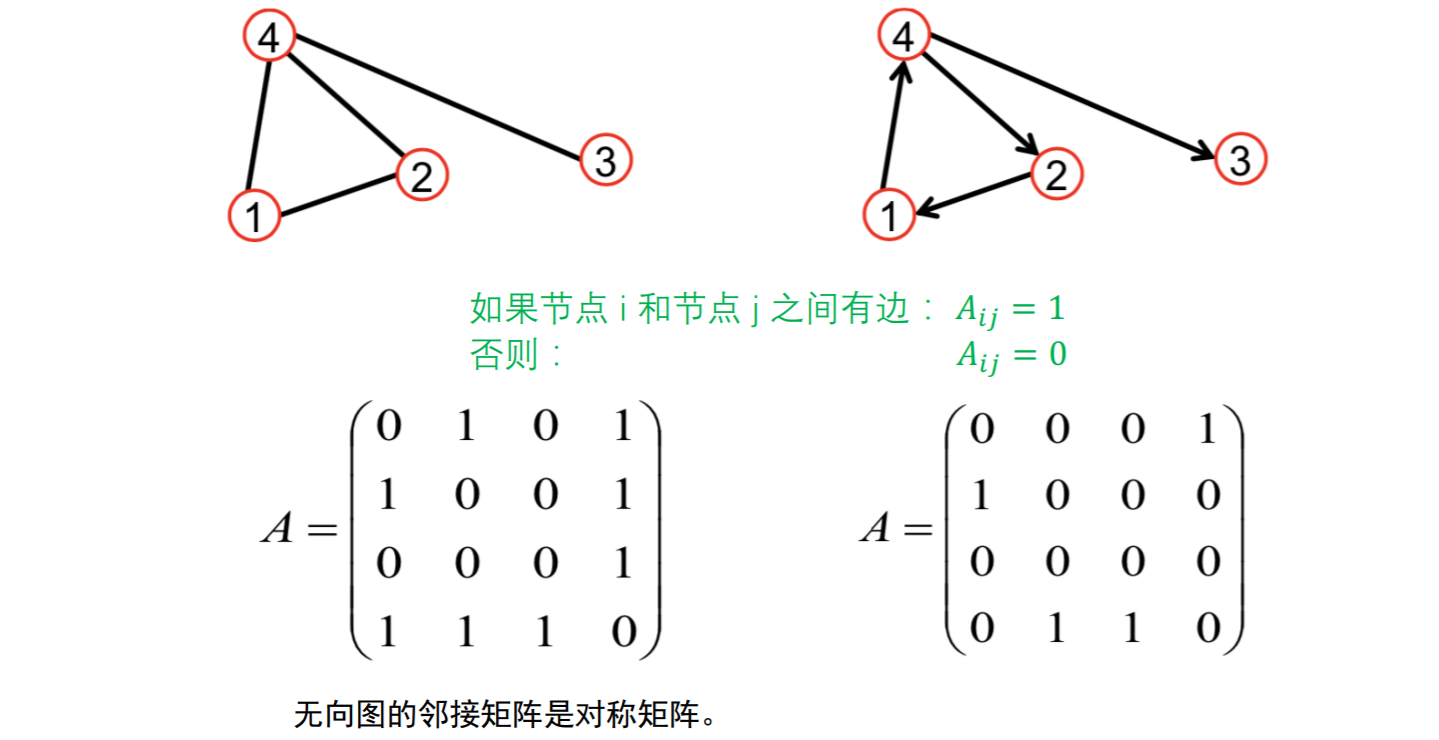
## 邻接表
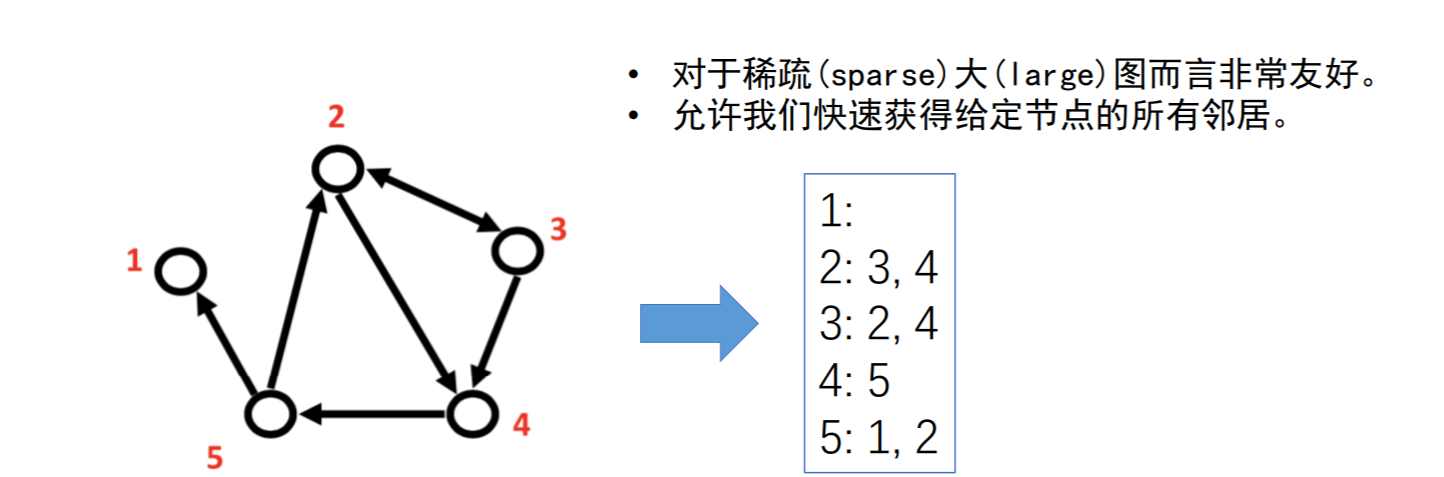
转换成邻接表时,需注意无向图还是有向图
## 边集
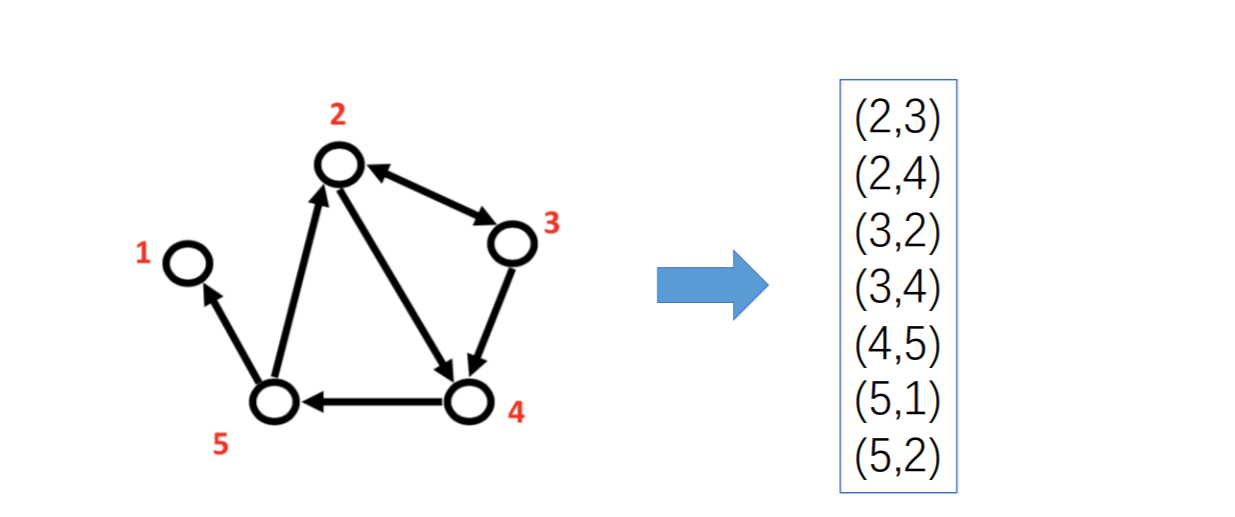
## 结构特征、节点特征、边特征
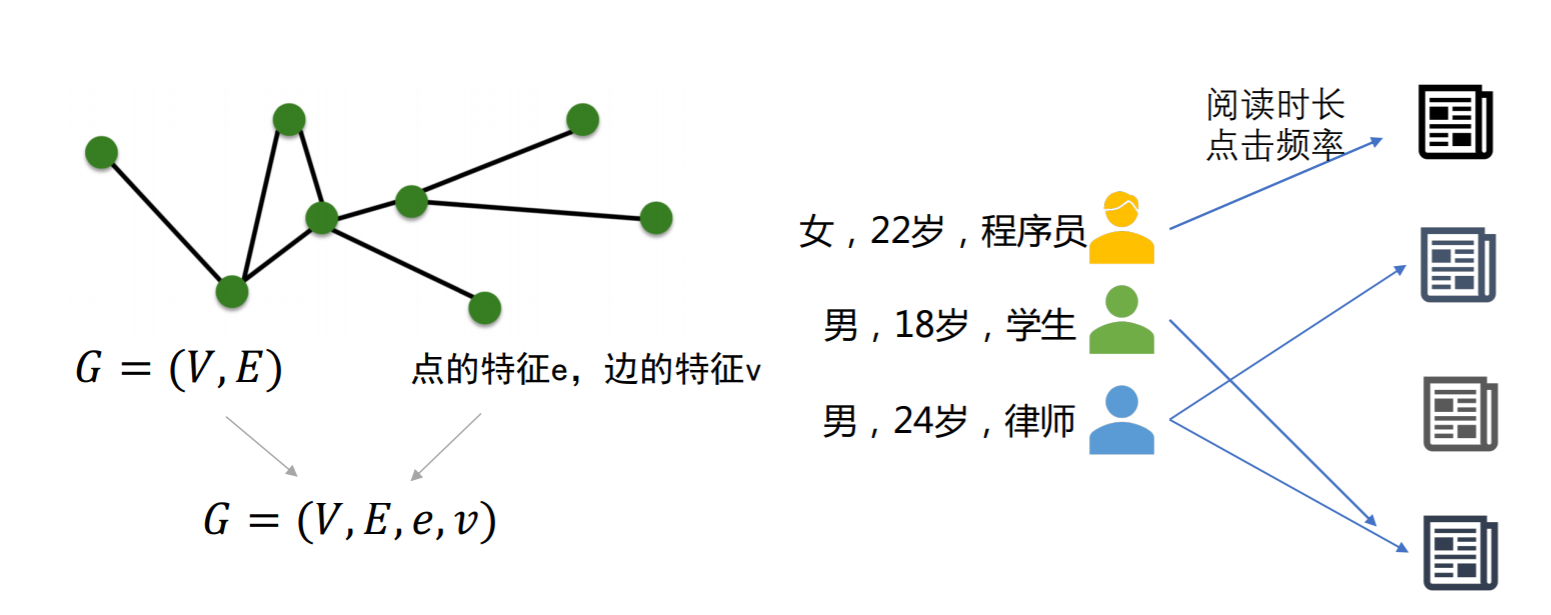
# 图学习
## 什么是图学习

## 图学习的优势
## 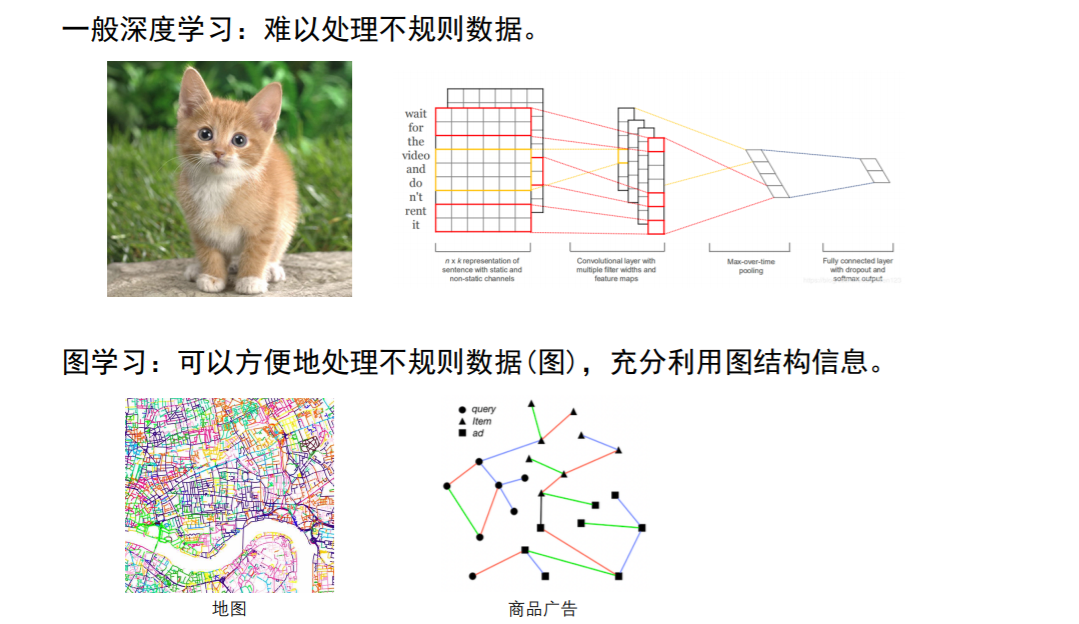
## 图学习的应用
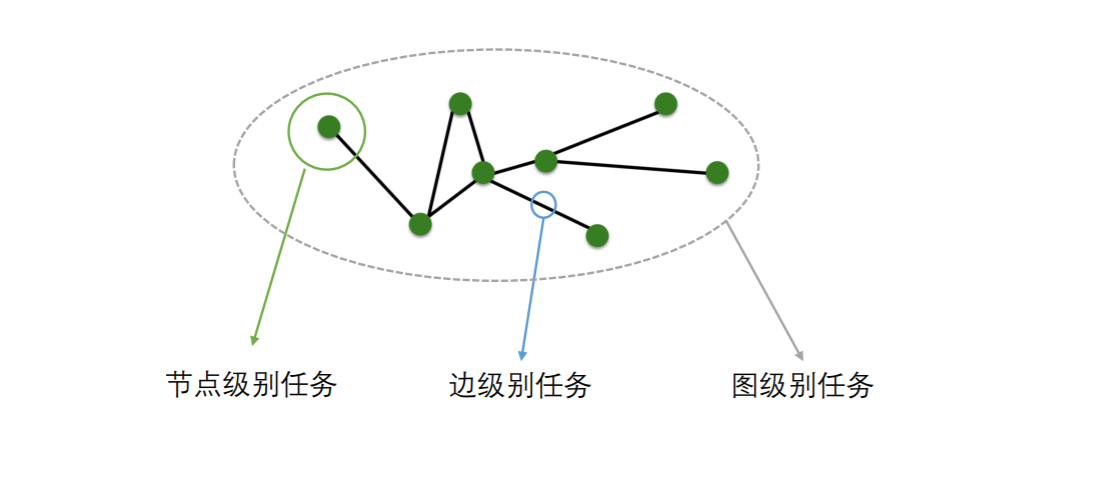
### 节点级任务
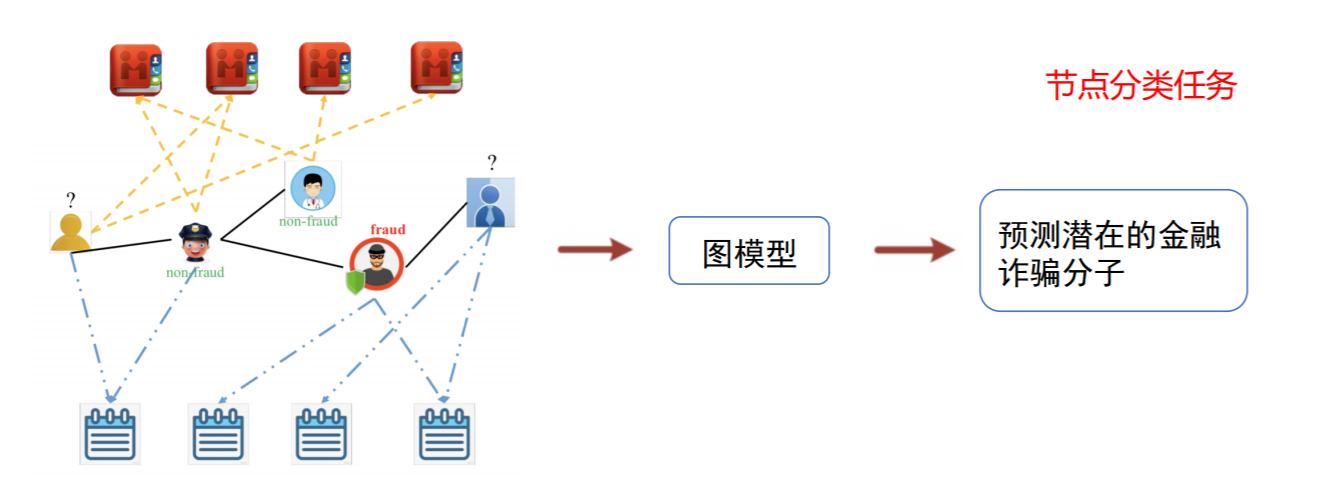
### 边级别任务
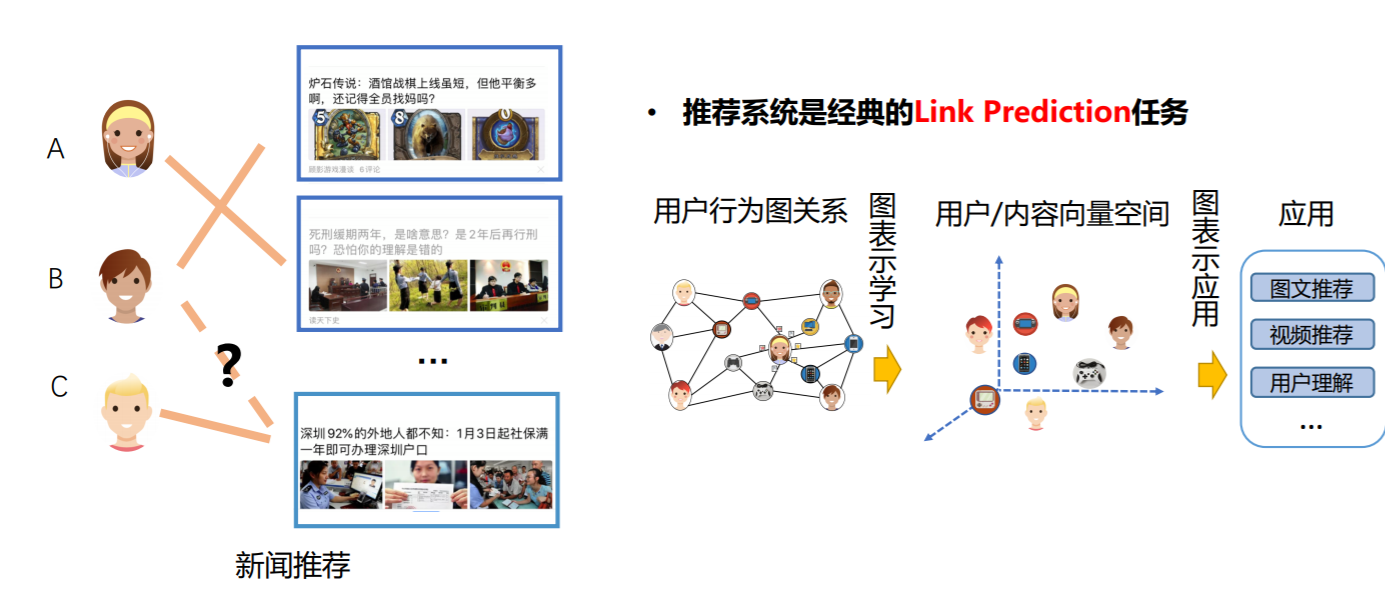
### 图级别任务
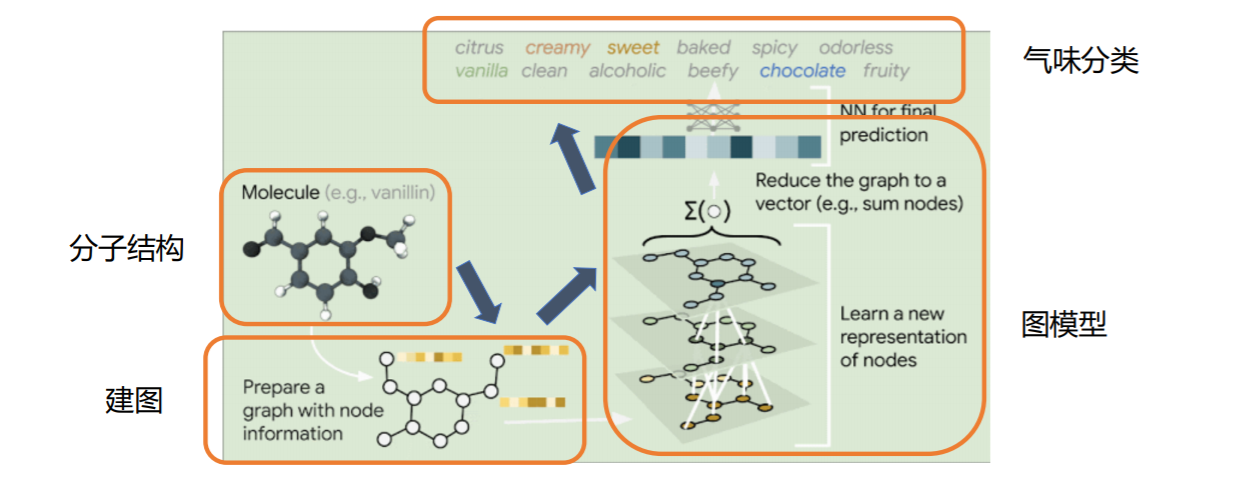
# 图游走类算法

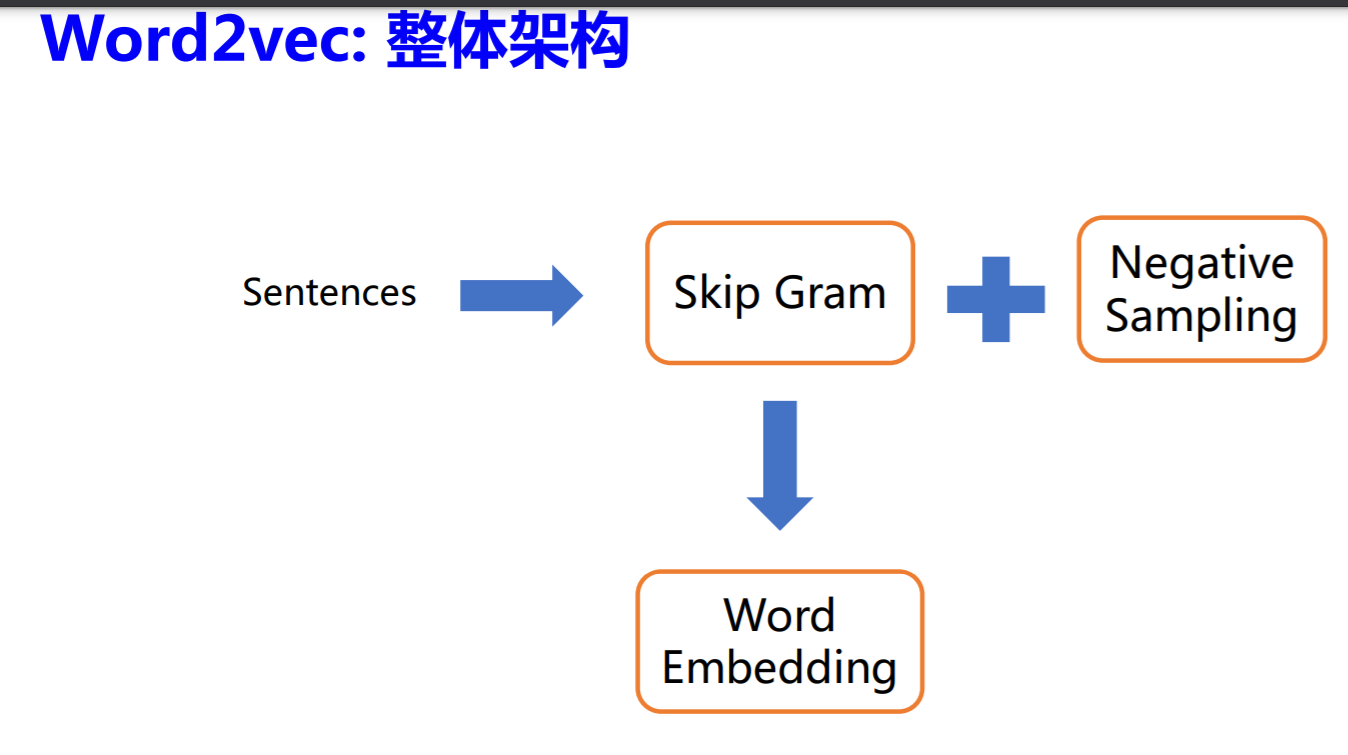
**图游走类算法最开始基于NLP 领域中的 Word2vec 模型**
## Word2vec: Skip Gram
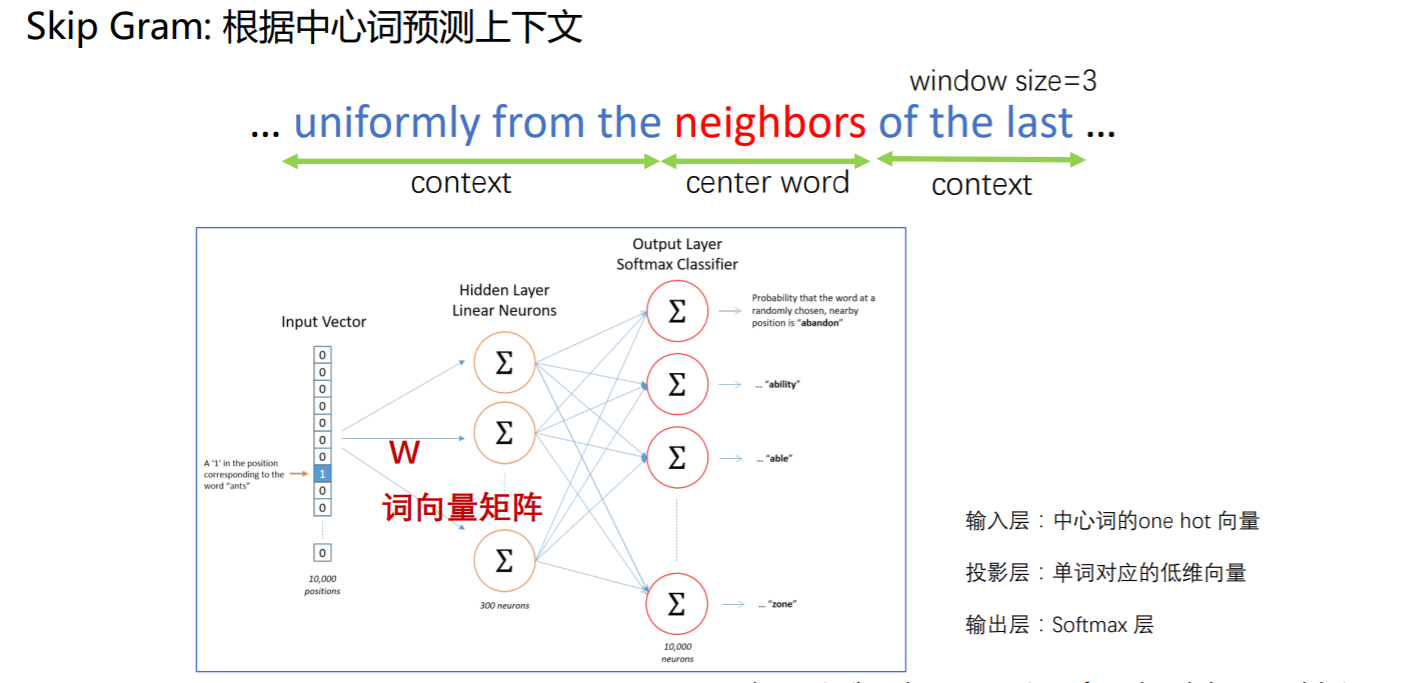

## DeepWalk