平面与三维网格求交

平面与网格相交

计算截面与三角形网格的相交可以分解为三角形面与平面的相交。而三角形面与平面的相交又可以分解为线段与平面的相交，那么现在问题就变为了线段与平面相交的计算。

直线–平面相交

在3D中，直线 L或者平行于平面π或者与平面π相交于一点。
　　描述L的函数是 $L = P(s) = P_0 + s(P_1-P_0) = P_0 + su$　　
　　描述平面π可以用平面上一点$V_0$和法线n表示

是否平行

如果直线与平面平行，则直线与平面不交
　　u表示直线的法线，如果$n·u=0$，那就意味着直线法向量 u垂直于平面法向量n。如果成立，直线 L和平面π平行，即或者不相交，或者完全在平面p内。通过验证L上是否存在点P在平面π内，可以判断L和平面π是否相交，也就是说是否满足隐式直线方程：$n·(P-V_0) = 0$。

直线与平面相较于平面内一点

如果直线和平面不平行，即直线L和平面π相交于点$P(s_I)$，利用类似于2D中两条直线相交的方法，我们可以计算出点P(sI)的值。如图所示：

图片

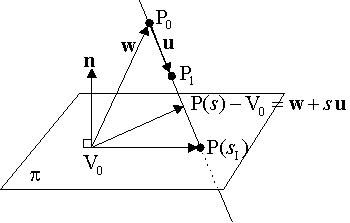
在相交点，当$w=P_0-V_0$，向量$P(s)-V_0 = w+su$垂直于n。这等同于点乘：$n · (w+su) = 0$。求解得出：
$$s_I＝\frac{-n \cdot w}{n\cdot u} = \frac{n \cdot (V_0-P0)}{n \cdot(P_1 - P_0)} $$

线段-直线相交

如果L 是从$P_0$到$P_1$的有限线段，我们必须检查sI是否满足 $0<= s_I <=1$，从而证明线段和平面是否相交。对于正方向的射线，当$s_I >=0$时，和平面相交。
而交点的坐标就等于$P(s_I ) = P_0 + s_I (P_1-P_0) = P_0 + s_I u$

需要处理的特殊情况是$n·（P_1-P_0) = 0$时，即线段与平面平行，这时由于除数为0不能计算，只需要判断P1在平面内即可（计算平面方程$n·(V_0 - P_0) = 0$）

float lineCrossFace(glm::vec3& point0,glm::vec3& point1,glm::vec3& v0,glm::vec3& normals)
{
    glm::vec3 ver = point1 - point0;
    float norDotVer = glm::dot(normals,ver);
    if (norDotVer == 0)
    {
        if (glm::dot(normals,(v0 - point1)) == 0)
        {
            return 1;
        }
        return -1;
    }
    float scale = (glm::dot(normals,(v0 - point0)))/norDotVer;
    return scale;
}

平面与网格相交实现

有了lineCrossFace,函数计算线段与平面相交，现在只需要将网格的每一条边作为一个线段遍历和平面求交就完成了。

 
 std::vector<glm::vec3>  sectionLine(std::vector<glm::vec4>& vertex,
                                                   std::vector<glm::ivec3>& indexArray,
                                                   glm::vec3& normal, glm::vec3& surfacePoint)
{
    std::vector<glm::vec3> sectionLine;
        normal = glm::normalize(normal);
        int crossPointIndex = 0;
        glm::vec3 curCrossVec[2];
        for (auto index : indexArray)
        {
            if (crossPointIndex == 2)
            {
                glm::vec3 point0 = curCrossVec[0];
                glm::vec3 point1 = curCrossVec[1];
                sectionLine.push_back(point0);
                sectionLine.push_back(point1);
            }
            crossPointIndex = 0;
            for (int lineIndex = 0;lineIndex < 3;lineIndex++)
            {
                float scale = lineCrossFace(vertex[index[lineIndex]],
                    vertex[index[(lineIndex+1)%3]],
                    surfacePoint,normal);
                if (scale <= 1 && scale > 0)
                {
                    curCrossVec[crossPointIndex] = scale * (vertex[index[(lineIndex+1)%3]] -
                            vertex[index[lineIndex]]) + vertex[index[lineIndex]];
                    ++crossPointIndex;
                }
                else if (scale == 0)
                {
                    curCrossVec[crossPointIndex] = vertex[index[lineIndex]];
                    ++crossPointIndex;
                }
 
                if ( crossPointIndex > 1)
                    break;
            }
        }
 
    return sectionLine;
}

最后编辑于：2017.12.10 06:25:39