简述题目
在一个系统中,有两种放射性原子A和B,原子A会衰变成原子B,而原子B也会衰变成原子A。严格上来说,这并不是一个“衰变”循环。一个更加恰当的解释应当是这个系统在保持能量不变的状态下可以在原子A和B中相互转化。而描述这个过程的速率方程是这样的:
(0.1)
(0.2)
利用这个方程解决这个原子数分别为NA和NB的系统,同时:
衰变周期
方程的解析
假设某类原子的衰变方程为:
(1.1)
然后对一段时间内的原子数量做泰勒展开:
=N(0)+\frac{dN}{dt}\cdot\Delta t+\frac{1}{2} \cdot \frac{d^2 N}{dt^2}+...)
只取前两项,则有:
\approx N(0)+\frac{dN}{dt}\cdot\Delta t .)
对(1.1)方程做近似:
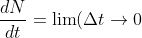\frac{N(t+\Delta t)-N(t)}{t}\approx\frac{N(t+\Delta t)-N(t)}{\Delta t})
所以有:
\approx N(t)+\frac{dN}{dt}\cdot\Delta t.)
由(1.1),有:
\approx N(t)-\frac{N(t)}{t_{dcy}}\cdot\Delta t)
题目方程解析
令:
=N_{B}(t)-N_{A}(t))
由(1.3)知:
\approx N_{A}(0)+\frac{dN_{A}}{dt}\cdot\Delta t)
\approx N_{B}(0)+\frac{dN_{B}}{dt}\cdot\Delta t)
由(1.5)(1.7)知:
\approx N_{A}(t)+\frac{dN_{A}}{dt}\cdot \Delta t \&=N_{A}(t)+\frac{1}{t_{dcy}}\cdot\Delta N(t)\cdot\Delta t\end{align})
\approx N_{B}(t)+\frac{dN_{B}}{dt}\cdot \Delta t \&=N_{B}(t)-\frac{1}{t_{dcy}}\cdot\Delta N(t)\cdot\Delta t\end{align})
代码模拟
- 我对c语言比较熟悉,所以先用c语言做模拟,之后再改成python
#include <stdio.h>
#include <math.h>
#define MAX 100
double dt; //time step
double t_decay; //time of decay
double t[MAX];
double N_A[MAX],N_B[MAX]; //number of atoms of A or B
double t_max;
double initialize(double Number_A[],double Number_B[],double time_decay,double dt) //initialize the system
{
printf("initial number of A-atom ->\n");
scanf("%lf",&Number_A[0]);
printf("initila number of B-atom ->\n");
scanf("%lf",&Number_B[0]);
printf("the time of decaying ->");
scanf("%lf",&time_decay);
printf("time step ->");
scanf("%lf",&dt);
t[0]=0.0;
return;
}
double calculate(double Number_A[],double Number_B[],double time_decay,double Delta_N)
{
int i;
for(i=0;i<MAX;i++)
{
Number_A[i+1]=Number_A[i]+((Number_B[i]-Number_A[i])/time_decay)*dt;
Number_B[i+1]=Number_B[i]- ((Number_B[i]-Number_A[i])/time_decay)*dt;
t[i+1]=t[i]+dt;
}
return;
}
double store(double Number_A[],double Number_B[],double t[]) //output the result
{
FILE *fp_out;
int i;
fp_out=fopen("decay_AB.dat","w");
for(i=0;i<MAX;i++)
{
fprintf(fp_out,"%lf\t%lf\t%lf\n",t[i],Number_A[i],Number_B[i]);
}
fclose(fp_out);
return;
}
void main()
{
initialize(N_A,N_B,t_decay,dt);
calculate(N_A,N_B,t_decay,Delta_N);
store(N_A,N_B,t);
}
- python语言部分
import numpy as np
import pylab as pl
Number_A=[]
Number_B=[]
t=[]
print("the number of A atoms ->")
number_a=input()
Number_A.append(number_a)
print("the number of B atoms ->")
number_b=input()
Number_B.append(number_b)
print("the time of decay ->")
t_decay=input()
print("the time step ->")
dt=input()
def Bigger(a,b):
if a>b:
return a
else:
return b
def Smaller(a,b):
if a>b:
return b
else:
return a
big=Bigger(Number_A[0],Number_B[0])
small=Smaller(Number_A[0],Number_B[0])
t.append(0.0)
for i in range(100):
NA=Number_A[i]+((Number_B[i]-Number_A[i])/t_decay)*dt
NB=Number_B[i]+((Number_A[i]-Number_B[i])/t_decay)*dt
tadd=t[i]+dt
Number_A.append(NA)
Number_B.append(NB)
t.append(tadd)
t_max=t[-1]
pl.plot(t,Number_A,'r')
pl.plot(t,Number_B,'g')
pl.title('the decay between A and B')
pl.xlabel('the time of decaying')
pl.ylabel('number of atoms')
pl.xlim(0.0,t_max)
pl.ylim(small,big)
pl.show()
实际模拟(用python做的模拟,比C要方便直观一些)
模拟1
A原子数为100,B原子数为80,衰变周期为1s,time step为0.05s,模拟结果为:

A原子数和B原子数逐渐趋于一致为90
模拟2
A原子数为100,B原子数为0,衰变周期为1.5s,time step为0.06s,模拟结果为:

A原子数与B原子数依旧趋于一致
结论
在这样一个系统中,两种原子的数量会逐渐趋于一致,且两种原子数量的变化率变为0.实际上是A原子与B原子处于相互转化的动态平衡中。