
本文cmd地址:经典检索算法:BM25原理
bm25 是什么?
bm25 是一种用来评价搜索词和文档之间相关性的算法,它是一种基于概率检索模型提出的算法,再用简单的话来描述下bm25算法:我们有一个query和一批文档Ds,现在要计算query和每篇文档D之间的相关性分数,我们的做法是,先对query进行切分,得到单词$q_i$,然后单词的分数由3部分组成:
- 单词$q_i$和D之间的相关性
- 单词$q_i$和D之间的相关性
- 每个单词的权重
最后对于每个单词的分数我们做一个求和,就得到了query和文档之间的分数。
bm25 解释
讲bm25之前,我们要先介绍一些概念。
二值独立模型 BIM
BIM(binary independence model)是为了对文档和query相关性评价而提出的算法,BIM为了计算$P(R|d,q)$,引入了两个基本假设:
假设1
一篇文章在由特征表示的时候,只考虑词出现或者不出现,具体来说就是文档d在表示为向量$\vec x=(x_1,x_2,...,x_n)$,其中当词$t$出现在文档d时,$x_t=1$,否在$x_t=0$。
假设2
文档中词的出现与否是彼此独立的,数学上描述就是$P(D)=\sum_{i=0}^n P(x_i)$
有了这两个假设,我们来对文档和query相关性建模:
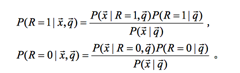
其中

接着因为我们最终得到的是一个排序,所以,我们通过计算文档和query相关和不相关的比率,也可得文档的排序,有下面的公式:

其中


由于每个 xt 的取值要么为 0 要么为 1,所以,我们可得到:
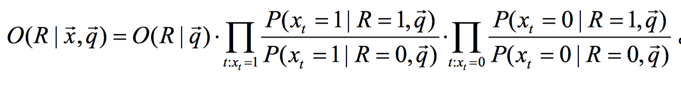
我们接着引入一些记号:


于是我们就可得到:

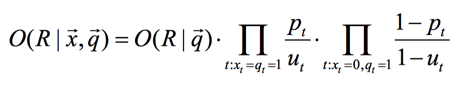
我们接着做下面的等价变换:
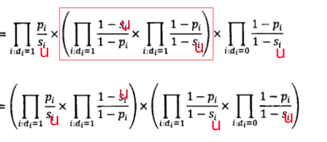

此时,公式中
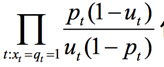

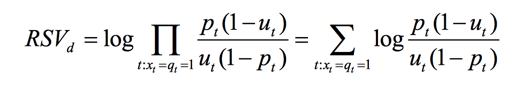
定义单个词的ct

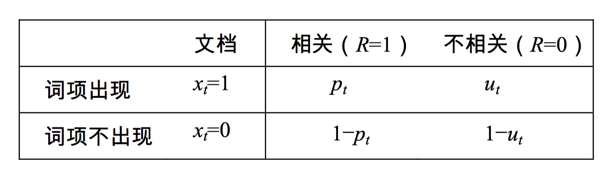
下一步我们要解决的就是怎么去估计pt和ut,看下表:

其中dft是包含词t的文档总数,于是

此时词t的ct值是:
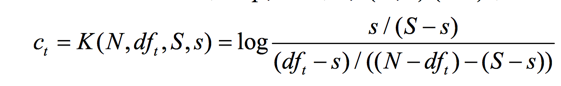
为了做平滑处理,我们都加上1/2,得到:

在实际中,我们很难知道t的相关文档有多少,所以假设S=s=0,所以:
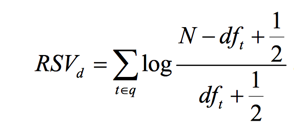
其中N是总的文档数,dft是包含t的文档数。
以上就是BIM的主要思想,后来人们发现应该讲BIM中没有考虑到的词频和文档长度等因素都考虑进来,就有了后面的BM25算法,下面按照
- 单词t和D之间的相关性
- 单词t和D之间的相关性
- 每个单词的权重
3个部分来介绍bm25算法。
单词权重
单词的权重最简单的就是用idf值,即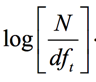
,也就是有多少文档包含某个单词信息进行变换。如果在这里使用 IDF 的话,那么整个 BM25 就可以看作是一个某种意义下的 TF-IDF,只不过 TF 的部分是一个复杂的基于文档和查询关键字、有两个部分的词频函数,还有一个就是用上面得到的ct值。
单词和文档的相关性
tf-idf中,这个信息直接就用“词频”,如果出现的次数比较多,一般就认为更相关。但是BM25洞察到:词频和相关性之间的关系是非线性的,具体来说,每一个词对于文档相关性的分数不会超过一个特定的阈值,当词出现的次数达到一个阈值后,其影响不再线性增长,而这个阈值会跟文档本身有关。
在具体操作上,我们对于词频做了”标准化处理“,具体公式如下:

其中,tftd 是词项 t 在文档 d 中的权重,Ld 和 Lave 分别是文档 d 的长度及整个文档集中文档的平均长度。k1是一个取正值的调优参数,用于对文档中的词项频率进行缩放控制。如果 k 1 取 0,则相当于不考虑词频,如果 k 1取较大的值,那么对应于使用原始词项频率。b 是另外一个调节参数 (0≤ b≤ 1),决定文档长度的缩放程度:b = 1 表示基于文档长度对词项权重进行完全的缩放,b = 0 表示归一化时不考虑文档长度因素。
单词和查询的相关性
如果查询很长,那么对于查询词项也可以采用类似的权重计算方法。
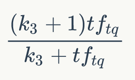
其中,tftq是词项t在查询q中的权重。这里k3 是另一个取正值的调优参数,用于对查询中的词项tq 频率进行缩放控制。
于是最后的公式是:

bm25 gensim中的实现
gensim在实现bm25的时候idf值是通过BIM公式计算得到的:

然后也没有考虑单词和query的相关性。

其中几个关键参数取值:
PARAM_K1 = 1.5
PARAM_B = 0.75
EPSILON = 0.25
此处EPSILON是用来表示出现负值的时候怎么获取idf值的。
总结下本文的内容:BM25是检索领域里最基本的一个技术,BM25 由三个核心的概念组成,包括词在文档中相关度、词在查询关键字中的相关度以及词的权重。BM25里的一些参数是经验总结得到的,后面我会继续介绍BM25的变种以及和其他文档信息(非文字)结合起来的应用。
参考
BM25 算法浅析
搜索之 BM25 和 BM25F 模型
经典搜索核心算法:BM25 及其变种
信息检索导论