作者：李飞腾链接：https://zhuanlan.zhihu.com/p/22473137
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。如果能二秒内在脑袋里解出下面的问题，本文便结束了。
已知：
J=(Xw-y)^T(Xw-y)=||Xw-y||^2
X\in R^{m \times n}, w \in R^{n \times 1}, y \in R^{m \times 1}
求：
\frac{\partial J}{\partial X}
\frac{\partial J}{\partial w}
\frac{\partial J}{\partial y}
到这里，请耐心看完下面的公式推导，无需长久心里建设。
首先，反向传播的数学原理是“求导的链式法则” :
设
f
g
x
(f \circ g)'(x) = f'(g(x))g'(x)
接下来介绍
矩阵、向量求导的维数相容原则
利用维数相容原则快速推导反向传播
编程实现前向传播、反向传播
卷积神经网络的反向传播
快速矩阵、向量求导
这一节展示如何使用链式法则、转置、组合等技巧来快速完成对矩阵、向量的求导
一个原则维数相容，实质是多元微分基本知识，没有在课本中找到下列内容，维数相容原则是我个人总结：
维数相容原则：通过前后换序、转置 使求导结果满足矩阵乘法且结果维数满足下式：
如果
x\in R^{m\times n}
f(x)\in R^1
\frac{\partial f(x)}{\partial x} \in R^{m\times n}
利用维数相容原则解上例：
step1：把所有参数当做实数来求导，
J=(Xw-y)^2
依据链式法则有
\frac{\partial J}{\partial X}=2(Xw-y)w
\frac{\partial J}{\partial w}=2(Xw-y)X
\frac{\partial J}{\partial y}=-2(Xw-y)
可以看出除了
\frac{\partial J}{\partial y}=-2(Xw-y)
\frac{\partial J}{\partial X}
\frac{\partial J}{\partial w}
step2：根据step1的求导结果，依据维数相容原则做调整：前后换序、转置
依据维数相容原则
\frac{\partial J}{\partial X} \in R^{m \times n}
\frac{\partial J}{\partial X} \in R^{m \times n} = 2(Xw-y)w
(Xw-y)\in R^{m \times 1}
w \in R^{n \times 1}
\frac{\partial J}{\partial X}=2(Xw-y)w^T
同理：
\frac{\partial J}{\partial w} \in R^{n \times 1}
\frac{\partial J}{\partial w} \in R^{n \times 1} = 2(Xw-y)X
(Xw-y) \in R^{m \times 1}
X \in R^{m \times n}
2X^T(Xw-y)
对于矩阵、向量求导：
“当做一维实数使用链式法则求导，然后做维数相容调整，使之符合矩阵乘法原则且维数相容”是快速准确的策略；
“对单个元素求导、再整理成矩阵形式”这种方式整理是困难的、过程是缓慢的，结果是易出错的（不信你试试）。
如何证明经过维数相容原则调整后的结果是正确的呢？直觉！简单就是美...快速反向传播：
神经网络的反向传播求得“各层”参数
W
b
接下来，展示不使用下标的记法（
W_{ij}
b_i
b_j
W
b
这里的标号，参考UFLDL教程 - Ufldl
前向传播：
z^{(l+1)}=W^{(l)}a^{(l)}+b^{(l)}
a^{(l+1)} =f(z^{(l+1)})
z^{(l)}
l
a^{(l)}
l
l+1
a^{(l)}
W^{(l)}
b^{(l)}
f()
z^{(l+1)}
a^{(l+1)}
设神经网络的损失函数为
J(W,b) \in R^1
\bigtriangledown_{W^{(l)}}J(W,b)=\frac{\partial J(W,b)}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial W^{(l)}}=\delta ^{(l+1)}(a ^{(l)})^T
\bigtriangledown_{b^{(l)}}J(W,b)=\frac{\partial J(W,b)}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial b^{(l)}}=\delta ^{(l+1)}
\frac{\partial J(W,b)}{\partial z^{(l+1)}}=\delta ^{(l+1)}
\frac{\partial z^{(l+1)}}{\partial W^{(l)}}=a ^{(l)}
\frac{\partial z^{(l+1)}}{\partial b^{(l)}}= 1
a ^{(l)}
(a ^{(l)})^{T}
如何求
\delta ^{(l)}=\frac{\partial J(W,b)}{\partial z^{(l)}}
\delta ^{(l)}=\frac{\partial J}{\partial z^{(l)}}=\frac{\partial J}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial a^{(l)}} \frac{\partial a^{(l)}}{\partial z^{(l)}}= ((W^{(l)})^{T}\delta ^{(l+1)}) \cdot f'(z^{(l)})
\frac{\partial J}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial a^{(l)}} = (W^{(l)})^T \delta ^{(l+1)}
\frac{\partial a^{(l)}}{\partial z^{(l)}} = f'(z^{(l)})
那么我们可以从最顶层逐层往下，便可以递推求得每一层的
\delta ^{(l)} = \frac{\partial J(W,b)}{\partial z^{(l)}}
注意：
\frac{\partial a^{(l)}}{\partial z^{(l)}} = f'(z^{(l)})
反向传播整个流程如下：
- 进行前向传播计算，利用前向传播公式，得到隐藏层和输出层 的激活值。
-
对输出层(第l
层)，计算残差：
（不同损失函数，结果不同，这里不给出具体形式）\delta ^{(l)} =\frac{\partial J(W,b)}{\partial z^{(l)}} - 对于的隐藏层，计算：l-1, l-2 , ... , 2
4) 计算各层参数\delta ^{(l)}=\frac{\partial J}{\partial z^{(l)}}=\frac{\partial J}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial a^{(l)}}\frac{\partial a^{(l)}}{\partial z^{(l)}}=((W^{(l)})^{T}\delta ^{(l+1)}) \cdot f'(z^{(l)})、W^{(l)}偏导数：b^{(l)}
\bigtriangledown_{W^{(l)}}J(W,b)=\frac{\partial J(W,b)}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial W^{(l)}}=\delta ^{(l+1)}(a ^{(l)})^T编程实现\bigtriangledown_{b^{(l)}}J(W,b)=\frac{\partial J(W,b)}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial b^{(l)}}=\delta ^{(l+1)}
大部分开源library（如：caffe，Kaldi/src/{nnet1,nnet2}）的实现通常把、W^{(l)}作为一个layer，激活函数b^{(l)}作为一个layer（如：sigmoid、relu、softplus、softmax）。f()
反向传播时分清楚该层的输入、输出即能正确编程实现,如：
(公式1)z^{(l+1)}=W^{(l)}a^{(l)}+b^{(l)}
(公式2)a^{(l+1)} =f(z^{(l+1)})
(1)式AffineTransform/FullConnected层，以下是伪代码：
注: out_diff =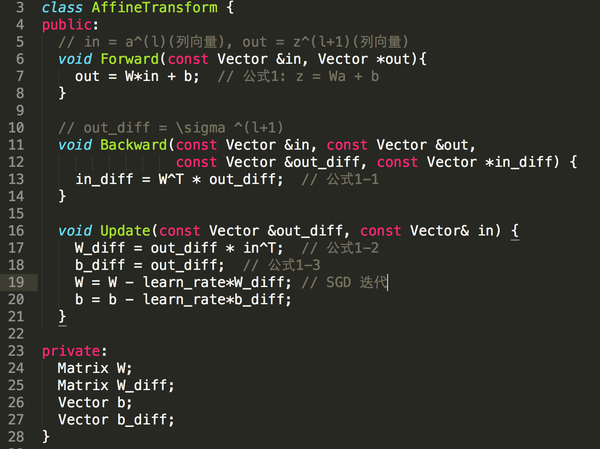
是上一层（Softmax 或 Sigmoid/ReLU的 in_diff）已经求得：\frac{\partial J}{\partial z^{(l+1)}}
（公式 1-1）in_diff = \frac{\partial J}{\partial a^{(l)}} = \frac{\partial J}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial a^{(l)}} = W^T * out_diff
（公式 1-2）W_diff =\frac{\partial J}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial W^{(l)}} = out_diff * in^T
（公式 1-3）b_diff =\frac{\partial J}{\partial z^{(l+1)}} \frac{\partial z^{(l+1)}}{\partial b^{(l)}} = out_diff * 1
(2)式激活函数层（以Sigmoid为例）
注：out_diff =
是上一层AffineTransform的in_diff，已经求得,\frac{\partial J}{\partial a^{(l+1)}}
在实际编程实现时，in、out可能是矩阵(通常以一行存储一个输入向量，矩阵的行数就是batch_size)，那么上面的C++代码就要做出变化（改变前后顺序、转置，把函数参数的Vector换成Matrix，此时Matrix out_diff 每一行就要存储对应一个Vector的diff，在update的时候要做这个batch的加和，这个加和可以通过矩阵相乘out_diffinput（适当的转置）得到。in_diff = \frac{\partial J}{\partial z^{(l+1)}} = \frac{\partial J}{\partial a^{(l+1)}} \frac{\partial a^{(l+1)}}{\partial z^{(l+1)}} = out_diff \cdot out \cdot (1-out)
如果熟悉SVD分解的过程，通过SVD逆过程就可以轻松理解这种通过乘积来做加和的技巧。
丢掉那些下标记法吧！
卷积层求导
卷积怎么求导呢？实际上卷积可以通过矩阵乘法来实现（是否旋转无所谓的，对称处理，caffe里面是不是有image2col），当然也可以使用FFT在频率域做加法。
那么既然通过矩阵乘法，维数相容原则*仍然可以运用，CNN求导比DNN复杂一些，要做些累加的操作。具体怎么做还要看编程时选择怎样的策略、数据结构。
快速矩阵、向量求导之维数相容大法已成
