这是系列教程的第二篇文章，公式的推导可能会愈加复杂，请认真分析！come on~

<h4>符号及标记</h4>

在进行数学运算之前，我们需要规定一些数学标记，方便接下来的讨论:

<h4>函数向量化</h4>
假设函数的向量化
如果我们的假设函数是：
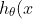=\theta_0 +\theta_1 x_1+\theta_2 x_2 +...+\theta_n x_n)

那么我们可以将上述式子向量化为：
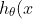=[\theta_0\ \theta_1\ \theta_2\ ...\theta_n]\cdot \begin{bmatrix}1 \ x_1 \ x_2 \ . \ . \ . \ x_n \end{bmatrix}= \theta^T\cdot X)
为了方便计算我们令：

举个例子，假设我们有这样一个训练集，每个训练样本的输入值都横向展开，如下所示：
} & x_1^{(1)} \ x_0^{(2)} & x_1^{(2)} \ x_0^{(3)} & x_1^{(3)} \end{bmatrix})
比如，第一个训练样本的数据集为

其次，参数的矩阵为：

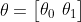
所以有：
 = X\cdot \theta)

代价函数的向量化
=\frac{1}{2m}\sum_{i=1}^{m}[h_{\theta}\left( x^i \right)-y^{(i)}]2=\frac{1}{2m}(X\theta - \vec{y})^T(X\theta - \vec{y}))

梯度下降算法的公式为：
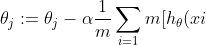-y^{(i)}]x{(i)}_{j})
其中 j=0,1,2, ... , m

将上述公式向量化，得到：

)
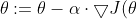=\begin{bmatrix} \frac{\partial}{\partial \theta_0}J(\theta) \ \frac{\partial}{\partial \theta_1}J(\theta) \ \frac{\partial}{\partial \theta_2}J(\theta) \ . \ . \ . \ \frac{\partial}{\partial \theta_m}J(\theta) \end{bmatrix})
其中：
=\frac{1}{m}\sum_{i=1}^{m}x_j{(i)}[h_{\theta}(x^{i})-y{(i)}])
通过分析角标之间的关系，我们可以将上述式子向量化为：
=\frac{1}{m}X^T[X \theta-\vec{y}\ ])

也就是说，我们的梯度下降算法表示为：

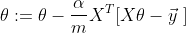
<h4>正规化方程</h4>
在对训练集应用梯度下降算法时，如果训练集的数据比较大，比如上千上万时，我们可能需要花费很长的时间来对训练集进行梯度下降，因此，在应用训练集数据进行训练前，我们需要对数据做一些预处理。

当数据值比较大的时候，我们可以对数据值这样处理：
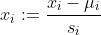
其中u_i是该数据样本的平均值，s_i是数据样本的极差（极差的概念请自行百度）。

当然我们也可以有自己的方法对数据进行处理，只要能方便我们对训练集应用梯度下降算法。不过在这里，我想要介绍利用正规化方程的方法来直接获得假设函数的参数值。

如果对于数据集X和y，存在参数集θ满足：
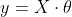
因此有：
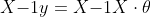
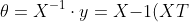^{-1}\cdot X^Ty = (X^T X)^{-1}XT y)

<h4>总结</h4>

下一篇教程就是实例代码的实战，上面的公式推导请好好消化，当然更多内容请参考机器学习。