Residual Network
原文:Deep Residual Learning for Image Recognition
博文参考:
- [译] Deep Residual Learning for Image Recognition (ResNet)
- Deep Residual Learning for Image Recognition(译)
- Resnet理解
- 残差网络ResNet笔记
代码参考:https://github.com/tornadomeet/ResNet
简介
深度卷积神经网络的出现使得图像分类问题的研究突飞猛进,但随之也出现了两个问题:
- 梯度消失、爆炸问题;
- 退化问题(degradation problem)。
前者,通常在初始化时,对数据进行归一化处理,以及添加正则化层处理。而后者,实验表明除了在浅层网络模型的基础上添加恒等映射(identity mapping)来构建深度网络模型之外,作者还没有找到其他的好的解决方案。
退化问题:随着网络层数的增加,模型准确度达到某一值后迅速降低,如下图一所示:
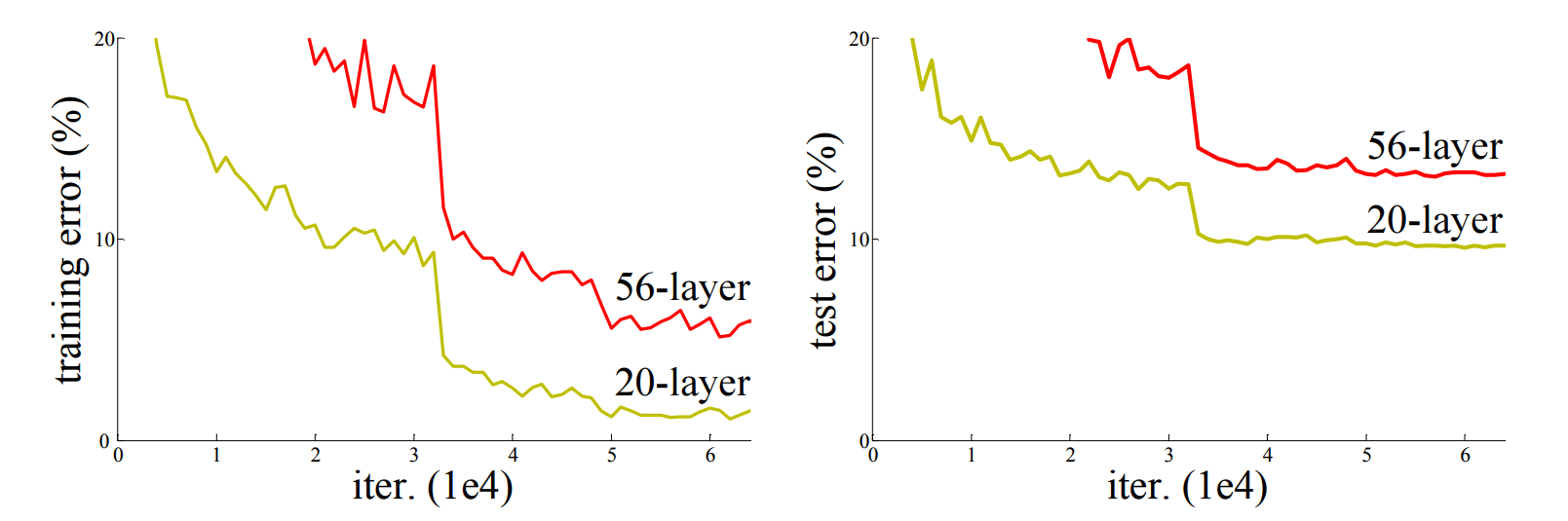
上图为不同深度的网络模型在CIFAR-10数据集上的误差变化曲线图。
因此,针对退化问题本文引入了深度残差学习框架(deep residual learning framework),让stacked layers拟合残差映射(residual mapping),而不是直接拟合the desired underlying mapping。
注:将the desired underlying mapping记为,现让stacked nonlinear layers拟合残差映射,即:
,则原映射(即the desired underlying mapping)
将改写为:
。
对此,作者假设残差映射相较于原映射更易优化。对于残差块,采用shortcut connection来实现,如下图二所示:
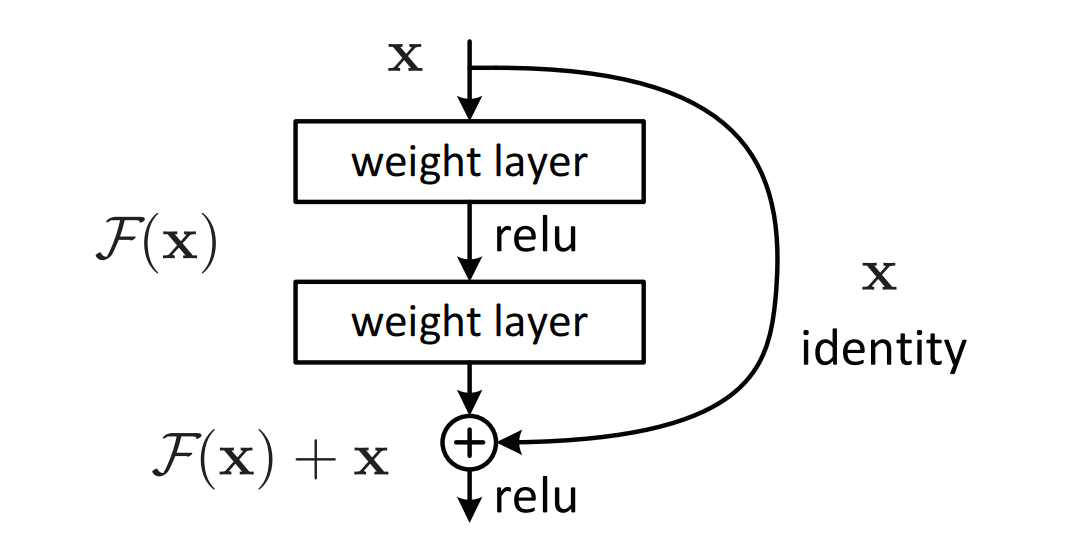
其中,shortcut connection仅执行恒等映射,且其输出添加至stacked layers的输出。恒等shortcut connection既不添加额外参数,也不增加计算的复杂度。
- 统计学:残差指预测值和观测值间的差距。
- 网络的一层视为
。
- 恒等映射:
。
- 残差映射:
,其中
为残差函数。
为输入,
为卷积分支的输出,
为整个结构的输出。
由于作者在文中已言明,目前还没有其他解决方案用于退化问题。因此,为了优化恒等映射(即通过stacked layer拟合很困难),作者提出残差映射方法。在原始的方法中,为了实现恒等映射,通过stacked layers来拟合。但在残差映射中,只需令残差函数
为0即可实现。
深度残差学习
残差学习
在简介部分已经说明了,原始的恒等映射需要多个非线性层来拟合,但在实际实现过程中很难实现。因此,作者引入了残差映射。理论上,只要恒等映射达到最佳时,则可迫使多个非线性层的权重趋向于0即可实现恒等映射。
虽然在实际情况中,恒等映射是不太可能为最佳的,但若存在最优的函数接更近于恒等映射而不是接近于0,则网络会更易发现扰动因素。实验表明学习到的残差函数响应值通常较小,同时也表明了恒等映射提供了合理的预处理,如下图三所示。
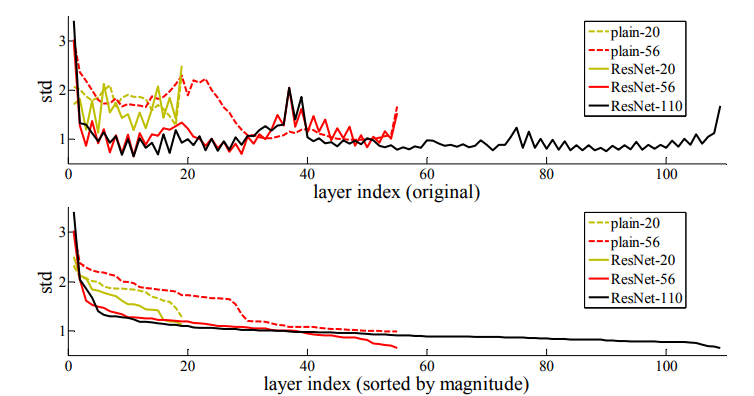
上图为在CIFAR-10数据集上各网络的层响应值的标准差变化曲线图。其中,响应值为每个大小为层的BN之后非线性之前的输出。上下两幅图其层的顺序有所不同:前者为原始顺序,后者为以响应值从大到小排列。
以shortcut的恒等映射
在每个stacked layer都使用残差学习,其结构如图二所示,数学表达式为:
其中,和
均为残差块所在层的输入与输出向量,函数
为训练残差映射所学习到的。
以图二的残差块为例,其残差函数为,其中
表示ReLU激活函数,出于简化省略偏置项。对于
运算,由一个shortcut connection和以element-wise方式累加实现的,其值为二阶非线性。
对于,要求
与
维数相同。若出现维数不同的情况,则在shortcut connection上添加一个线性投影
来匹配维度:
注:残差函数同样适用于卷积层,且形式灵活。
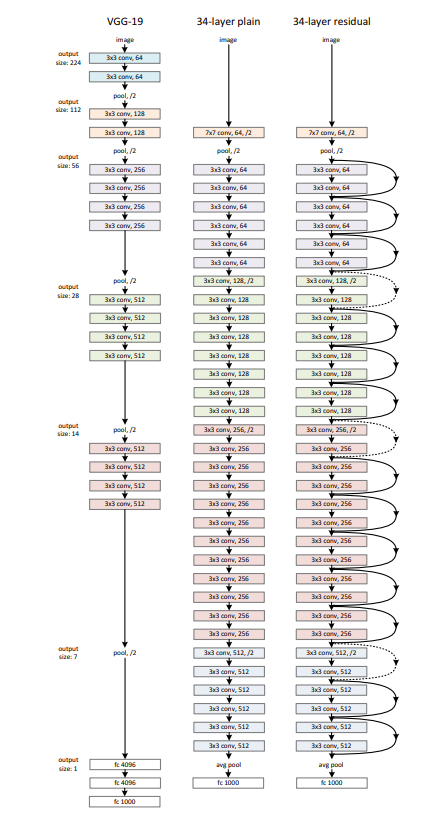
网络结构
Plain Network
卷积层的filter大多为大小,且遵循两个设计原则:
- 对于相同大小的输出特征图,其层需含有相同数量的filter;
- 若特征图的大小减半,则filter的数量需翻倍,以保证每层的时间复杂度。
在卷积层上以步长为2进行下采样操作。在网络末端以全局的均值池化层和1000个激活函数为softmax函数的全连接层结束。含权重的层总数为34层。
ResNet
在plain network的基础上添加shortcut connection,将网络变为ResNet。当维度增加时,可考虑如下两个方法:
- 使用0来填补增加的维数,且此方法不会引入额外参数;
- 在shortcut connection上添加一个线性投影
来匹配维数(通过卷积核大小为
的卷积实现)。
对于以上两种方法,其步长均为2。
注:
对于添加线性投影,实际上有两种情况:
- 只对维数增加的数据进行处理;
- 对所有数据进行处理。
后续实验表明,后者比前者效果好,但引入了额外参数,且线性投影与退化问题无关。因此,为了降低内存的使用、时间复杂度以及模型大小,作者采用前者进行处理。