首先我们将theta作为横坐标，omega作为纵坐标，同时变化F_D的参数，比较这两种情况下摆的混沌效应．
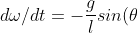-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t))

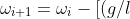• sin\theta_i-q\omega_i+F_Dsin(\Omega_Dt_i)]\Delta t)
• 
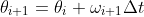
• if \theta_{i+1} is out of the range[-pi,pi],add or substract 2pi to keep it in the range.
• 
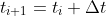
• Repeat

代码实现

def swing(self):
        loop = True
        i = 0
        while(loop):
            self.omega.append(self.omega[i] + (-self.g_l * math.sin(self.theta[i]) - self.q * self.omega[i] +
                                                   self.f_d * math.sin(self.omega_d * self.t[i])) * self.dt)
            self.temp = self.theta[i] + self.omega[i + 1] * self.dt
            if math.pi < self.temp:
                self.temp -= 2 * math.pi
            elif - math.pi > self.temp:
                self.temp += 2 * math.pi
            self.theta.append(self.temp)
            self.t.append(self.t[i] + self.dt)
            i += 1
            if self.total_time < self.t[i]:
                loop = False

Then we only plot omega versus theta only at times that are in phase with the driving force.
That is,we only display the point when
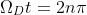
where n is an integer.

• 也就是说，当满足
  时，我们就将相应的点放置上去

代码实现

def Omega2Theta(self):
        self.swing()
        loop = True
        i = 0
        n = 0
        while(loop):
            # omega_D * t = 2 * pi * n
            if (self.t[i] > (2*n+1)*math.pi/self.omega_d):
                n += 1
            if (abs(self.t[i] - 2 * n * math.pi/self.omega_d) < (self.dt/2)):
                self.theta_ps.append(self.theta[i])
                self.omega_ps.append(self.omega[i])
            i += 1
            if self.total_time < self.t[i]:
                loop = False

接下来让我们变化一下参数：

我们观察一下\theta与ｔ在变化的驱动力下的关系图

• 致谢
  　卢江玮的代码助攻～