CNN on TensorFlow
本文大部分内容均参考于:
An Intuitive Explanation of Convolutional Neural Networks
知乎:「为什么 ReLU 要好过于 tanh 和 sigmoid function?」
Deep MNIST for Experts
TensorFlow Python API 「tf.nn」
Build a Multilayer Convolutional Network
在 TensorFlow 官方的 tutorials 中,我们使用 softmax 模型在 MNIST 数据集上得到的结果只有 91% 的正确率,实在太糟糕。所以,我们将使用一个稍微复杂的模型:CNN(卷积神经网络)来改善实验效果。在 CNN 主要有四个操作:
- 卷积
- 非线性处理(ReLU)
- 池化或者亚采样
- 分类(全连接层)
这些操作对于各个卷积神经网络来说都是基本组件,因此理解它们的工作原理有助于充分了解卷积神经网络。下面我们将会尝试理解各步操作背后的原理。
What's CNN
Convolution
卷积的主要目的是为了从输入图像中提取特征。卷积可以通过从输入的一小块数据中学到图像的特征,并可以保留像素间的空间关系。让我们举个例子来尝试理解一下卷积是如何处理图像的:
正如我们上面所说,每张图像都可以看作是像素值的矩阵。考虑一下一个 5 x 5 的图像,它的像素值仅为 0 或者 1(注意对于灰度图像而言,像素值的范围是 0 到 255,下面像素值为 0 和 1 的绿色矩阵仅为特例):
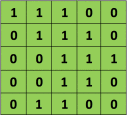
同时,考虑下另一个 3 x 3 的矩阵,如下所示:

接下来,5 x 5 的图像和 3 x 3 的矩阵的卷积可以按下图所示的动画一样计算:
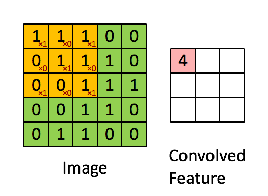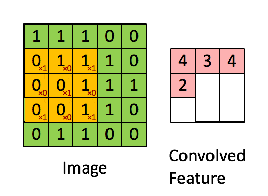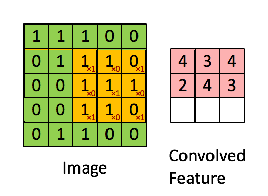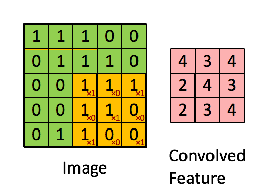
现在停下来好好理解下上面的计算是怎么完成的。我们用橙色的矩阵在原始图像(绿色)上滑动,每次滑动一个像素(也叫做「步长」),在每个位置上,我们计算对应元素的乘积(两个矩阵间),并把乘积的和作为最后的结果,得到输出矩阵(粉色)中的每一个元素的值。注意,3 x 3 的矩阵每次步长中仅可以看到输入图像的一部分。
在 CNN 的术语中,3x3 的矩阵叫做「滤波器」(filter) 或「核」(kernel) 或者 「特征检测器」(feature detector),通过在图像上滑动滤波器并计算点乘得到矩阵叫做「卷积特征」(Convolved Feature) 或者 「激活图」(Activation Map) 或者 「特征图」(Feature Map)。记住,滤波器在原始输入图像上的作用是特征检测器。
从上面图中的动画可以看出,对于同样的输入图像,不同值的滤波器将会生成不同的特征图。比如,对于下面这张输入图像:

在下表中,我们可以看到不同滤波器对上图卷积的效果。正如表中所示,通过在卷积操作前修改滤波矩阵的数值,我们可以进行诸如边缘检测、锐化和模糊等操作 —— 这表明不同的滤波器可以从图中检测到不同的特征,比如边缘、曲线等。

另一个直观理解卷积操作的好方法是看下面这张图的动画:

滤波器(红色框)在输入图像滑过(卷积操作),生成一个特征图。另一个滤波器(绿色框)在同一张图像上卷积可以得到一个不同的特征图。注意卷积操作可以从原图上获取局部依赖信息。同时注意这两个不同的滤波器是如何从同一张图像上生成不同的特征图。记住上面的图像和两个滤波器仅仅是我们上面讨论的数值矩阵。
在实践中,CNN 会在训练过程中学习到这些滤波器的值(尽管我们依然需要在训练前指定诸如滤波器的个数、滤波器的大小、网络架构等参数)。我们使用的滤波器越多,提取到的图像特征就越多,网络所能在未知图像上识别的模式也就越好。
特征图的大小(卷积特征)由下面三个参数控制,我们需要在卷积前确定它们:
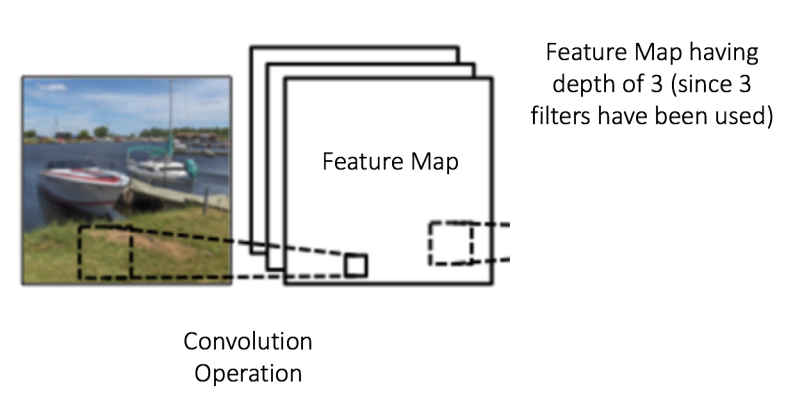
深度(Depth):深度对应的是卷积操作所需的滤波器个数。在下图的网络中,我们使用三个不同的滤波器对原始图像进行卷积操作,这样就可以生成三个不同的特征图。你可以把这三个特征图看作是堆叠的 2d 矩阵,那么,特征图的「深度」就是 3。
步长(Stride):步长是我们在输入矩阵上滑动滤波矩阵的像素数。当步长为 1 时,我们每次移动滤波器一个像素的位置。当步长为 2 时,我们每次移动滤波器会跳过 2 个像素。步长越大,将会得到更小的特征图。
零填充(Zero-padding):有时,在输入矩阵的边缘使用零值进行填充,这样我们就可以对输入图像矩阵的边缘进行滤波。零填充的一大好处是可以让我们控制特征图的大小。使用零填充的也叫做泛卷积,不适用零填充的叫做严格卷积。
ReLU
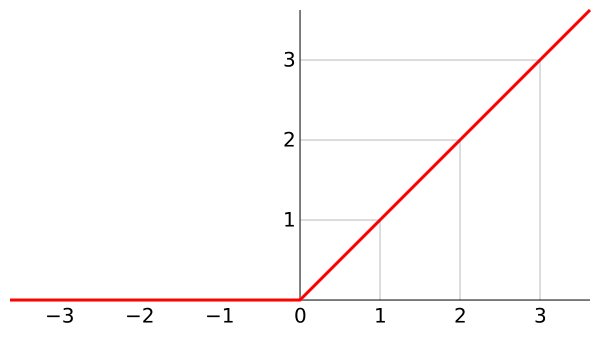
ReLU表示修正线性单元(Rectified Linear Unit),是一个非线性操作。
-
为什么要引入非线性激励函数?
如果不用激励函数(其实相当于激励函数是 $f(x) = x$ ),在这种情况下你每一层输出都是上层输入的线性函数,很容易验证,无论你神经网络有多少层,输出都是输入的线性组合,与没有隐层效果相当,这种情况就是最原始的感知机(Perceptron)了。
正因为上面的原因,我们决定引入非线性函数作为激励函数,这样深层神经网络就有意义了(不再是输入的线性组合,可以逼近任意函数)。最早的想法是 sigmoid 函数或者 tanh 函数,输出有界,很容易充当下一层输入(以及一些人的生物解释balabala)。
-
为什么要引入 ReLU 而不是其他的非线性函数(例如 Sigmoid 函数)?
- 采用 sigmoid 等函数,算激活函数时(指数运算),计算量大,反向传播求误差梯度时,求导涉及除法,计算量相对大,而采用Relu激活函数,整个过程的计算量节省很多。
- 对于深层网络,sigmoid 函数反向传播时,很容易就会出现梯度消失的情况(在sigmoid接近饱和区时,变换太缓慢,导数趋于0,这种情况会造成信息丢失),从而无法完成深层网络的训练。
- Relu 会使一部分神经元的输出为 0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生(以及一些人的生物解释balabala)。
当然现在也有一些对 relu 的改进,比如 prelu,random relu等,在不同的数据集上会有一些训练速度上或者准确率上的改进,具体的可以找相关的paper看。
(多加一句,现在主流的做法,会多做一步 batch normalization,尽可能保证每一层网络的输入具有相同的分布。而最新的 paper,他们在加入bypass connection 之后,发现改变 batch normalization 的位置会有更好的效果。)
-
ReLU 的优点与缺点?
优点:
- 解决了gradient vanishing问题 (在正区间)
- 计算速度非常快,只需要判断输入是否大于0
- 收敛速度远快于sigmoid和tanh
缺点:
- ReLU 的输出不是 zero-centered
- Dead ReLU Problem,指的是某些神经元可能永远不会被激活,导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化,这种情况比较少见 (2) learning rate 太高导致在训练过程中参数更新太大,不幸使网络进入这种状态。解决方法是可以采用 Xavier 初始化方法,以及避免将 learning rate 设置太大或使用 adagrad 等自动调节 learning rate 的算法。
几十年的机器学习发展中,我们形成了这样一个概念:非线性激活函数要比线性激活函数更加先进。
尤其是在布满 Sigmoid 函数的 BP 神经网络,布满径向基函数的 SVM 神经网络中,往往有这样的幻觉,非线性函数对非线性网络贡献巨大。
该幻觉在 SVM 中更加严重。核函数的形式并非完全是 SVM 能够处理非线性数据的主力功臣(支持向量充当着隐层角色)。
那么在深度网络中,对非线性的依赖程度就可以缩一缩。另外,在上一部分提到,稀疏特征并不需要网络具有很强的处理线性不可分机制。
综合以上两点,在深度学习模型中,使用简单、速度快的线性激活函数可能更为合适。
ReLU 操作可以从下面的图中理解。这里的输出特征图也可以看作是“修正”过的特征图。

所谓麻雀虽小,五脏俱全,ReLU虽小,但也是可以改进的。
ReLU的种类
ReLU的区分主要在负数端,根据负数端斜率的不同来进行区分,大致如下图所示。
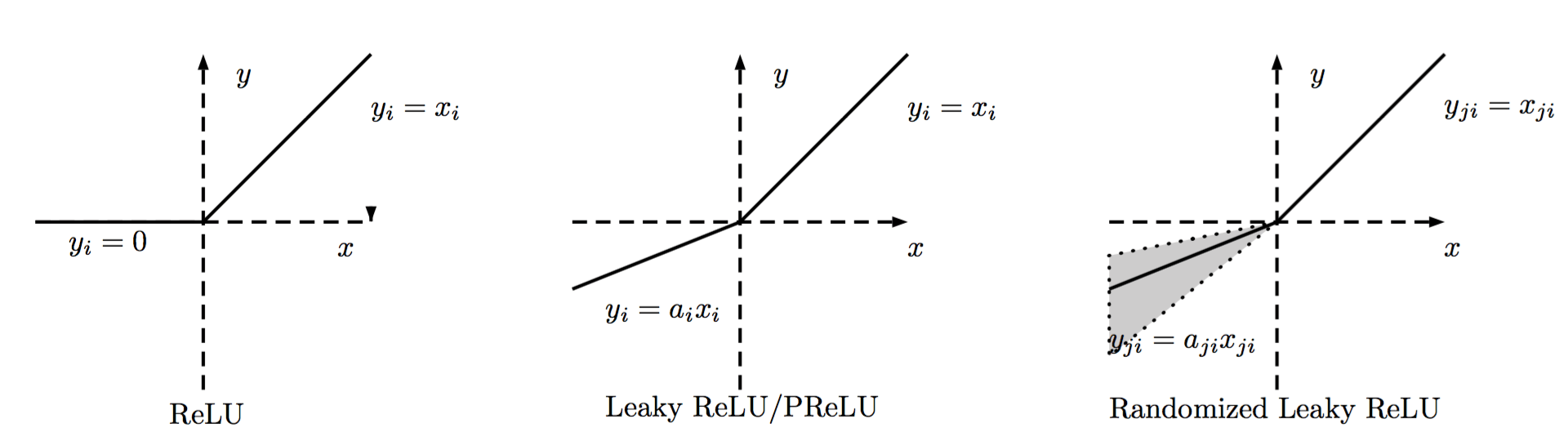
普通的ReLU负数端斜率是0,Leaky ReLU则是负数端有一个比较小的斜率,而PReLU则是在后向传播中学习到斜率。而Randomized Leaky ReLU则是使用一个均匀分布在训练的时候随机生成斜率,在测试的时候使用均值斜率来计算。
效果
其中,NDSB 数据集是 Kaggle 的比赛,而 RReLU 正是在这次比赛中崭露头角的。
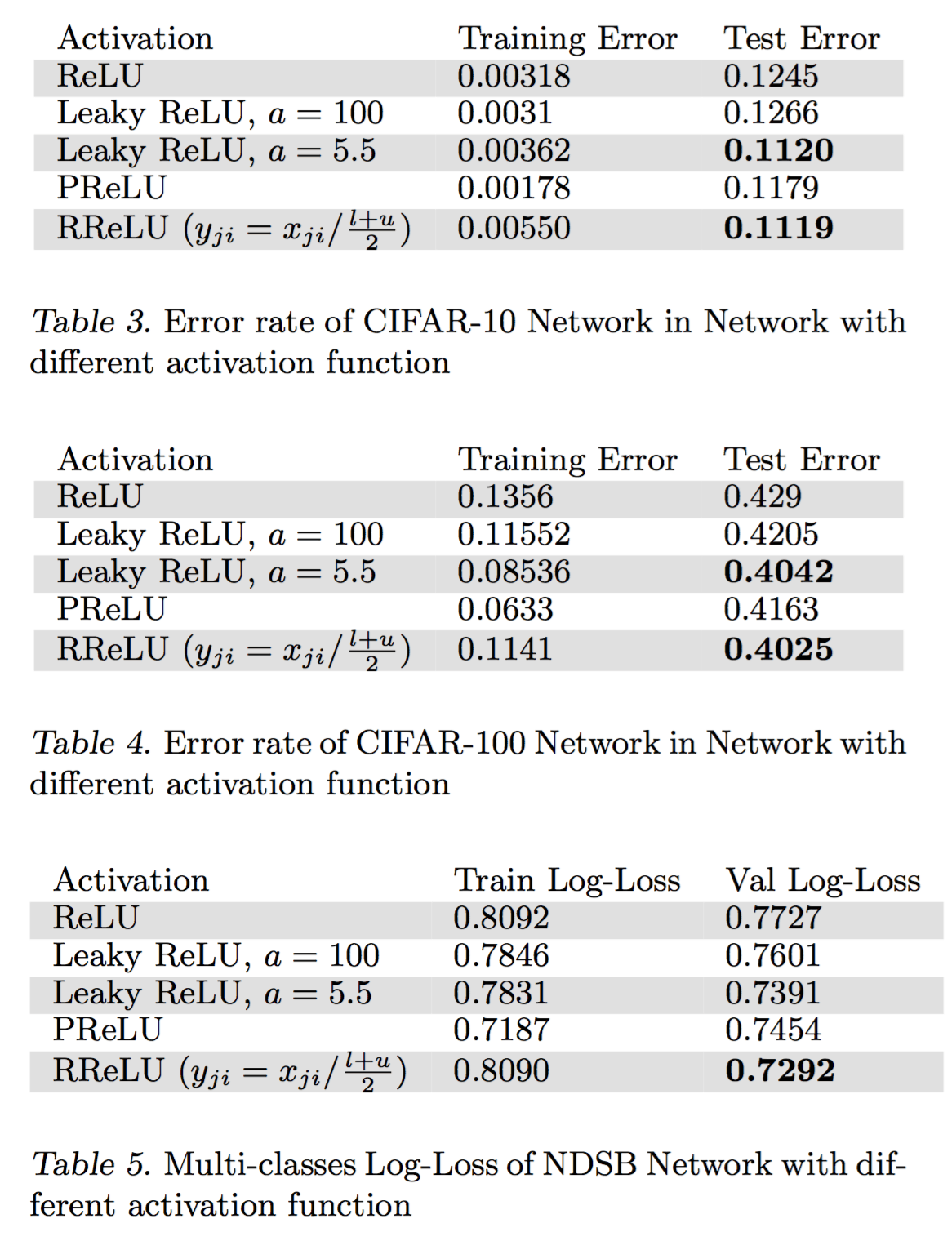
通过上述结果,可以看到四点:
- 对于 Leaky ReLU 来说,如果斜率很小,那么与 ReLU 并没有大的不同,当斜率大一些时,效果就好很多。
- 在训练集上,PReLU 往往能达到最小的错误率,说明 PReLU 容易过拟合。
- 在 NSDB 数据集上 RReLU 的提升比 cifar10 和 cifar100 上的提升更加明显,而 NSDB 数据集比较小,从而可以说明,RReLU在与过拟合的对抗中更加有效。
- 对于 RReLU 来说,还需要研究一下随机化得斜率是怎样影响训练和测试过程的。
参考文献
[1]. Xu B, Wang N, Chen T, et al. Empirical evaluation of rectified activations in convolutional network[J]. arXiv preprint arXiv:1505.00853, 2015.
Pooling
空间池化(Spatial Pooling)(也叫做亚采用或者下采样)降低了各个特征图的维度,但可以保持大部分重要的信息。空间池化有下面几种方式:最大化、平均化、加和等等。
对于最大池化(Max Pooling),我们定义一个空间邻域(比如,2x2 的窗口),并从窗口内的修正特征图中取出最大的元素。除了取最大元素,我们也可以取平均(Average Pooling)或者对窗口内的元素求和。在实际中,最大池化被证明效果更好一些。
下面的图展示了使用 2x2 窗口在修正特征图(在卷积 + ReLU 操作后得到)使用最大池化的例子。
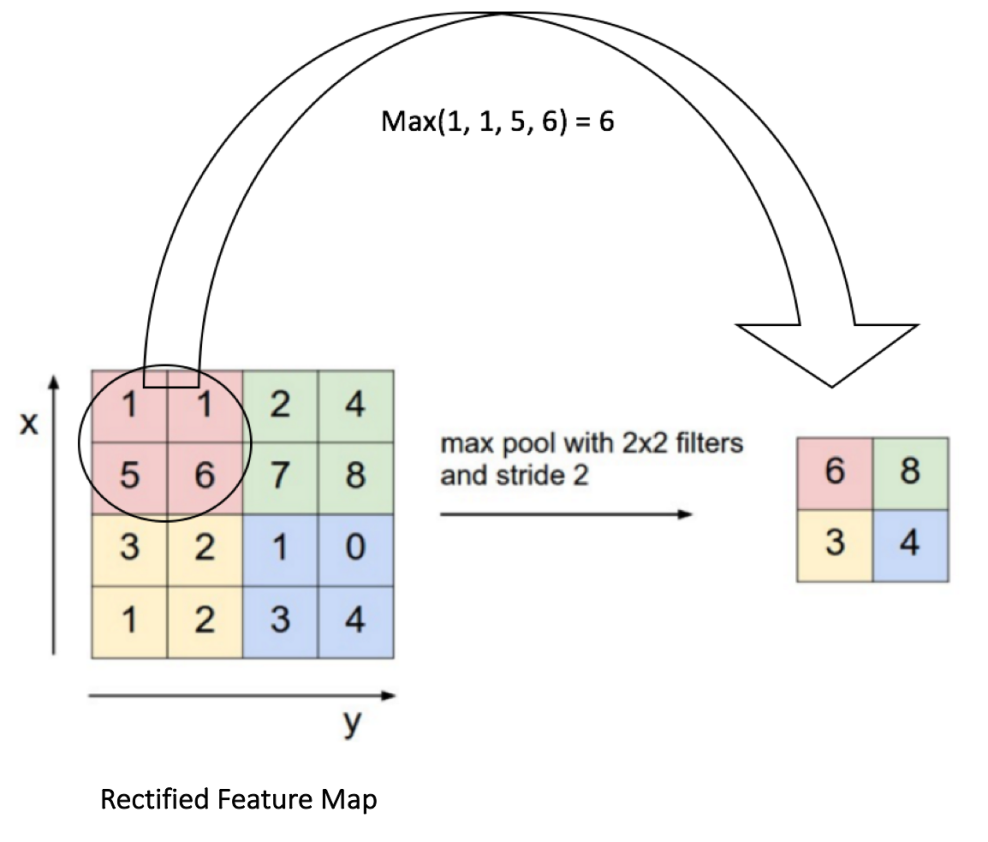
我们以 2 个元素(也叫做“步长”)滑动我们 2x2 的窗口,并在每个区域内取最大值。如上图所示,这样操作可以降低我们特征图的维度。
在下图展示的网络中,池化操作是分开应用到各个特征图的(注意,因为这样的操作,我们可以从三个输入图中得到三个输出图)。
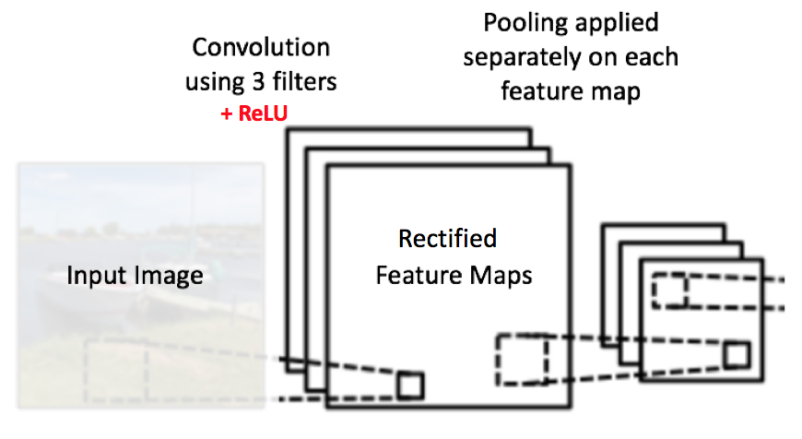
下图展示了我们在 ReLU 操作之后得到的修正特征图的池化操作的效果:
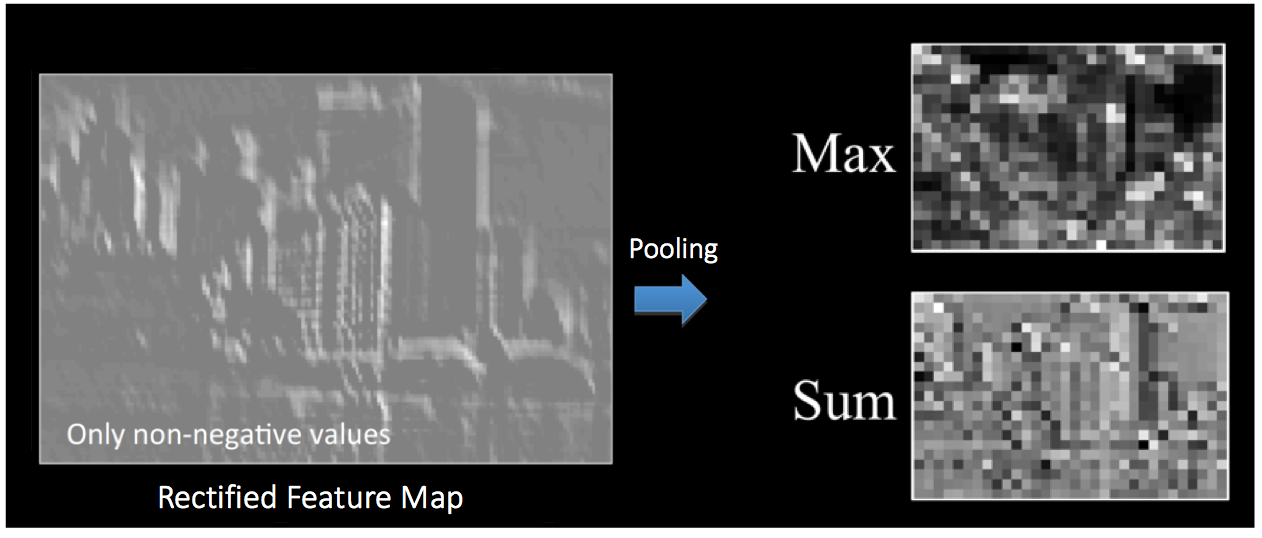
池化函数可以逐渐降低输入表示的空间尺度。特别地,Pooling 的好处是:
使输入表示(特征维度)变得更小,并且网络中的参数和计算的数量更加可控的减小,因此,可以控制过拟合。
使网络对于输入图像中更小的变化、冗余和变换变得不变性(输入的微小冗余将不会改变池化的输出——因为我们在局部邻域中使用了最大化/平均值的操作)。
-
帮助我们获取图像最大程度上的尺度不变性(准确的词是“不变性”)。它非常的强大,因为我们可以检测图像中的物体,无论它们位置在哪里。
到目前为止我们了解了卷积、ReLU 和池化是如何操作的。理解这些层是构建任意 CNN 的基础是很重要的。正如下图所示,我们有两组卷积、ReLU & 池化层 —— 第二组卷积层使用六个滤波器对第一组的池化层的输出继续卷积,得到一共六个特征图。接下来对所有六个特征图应用 ReLU。接着我们对六个修正特征图分别进行最大池化操作。
这些层一起就可以从图像中提取有用的特征,并在网络中引入非线性,减少特征维度,同时保持这些特征具有某种程度上的尺度变化不变性。
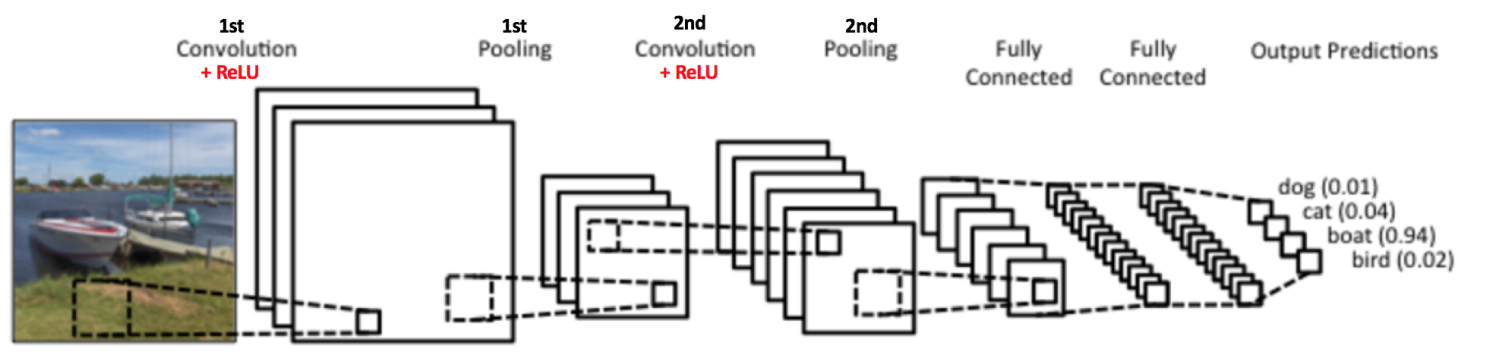
第二组池化层的输出作为全连接层的输入,接下来我们将介绍全连接层。
Connect
全连接层是传统的多层感知器,在输出层使用的是 softmax 激活函数(也可以使用其他像 SVM 的分类器,但在本文中只使用 softmax)。「全连接」(Fully Connected) 这个词表明前面层的所有神经元都与下一层的所有神经元连接。
卷积和池化层的输出表示了输入图像的高级特征。全连接层的目的是为了使用这些特征把输入图像基于训练数据集进行分类。比如,在下面图中我们进行的图像分类有四个可能的输出结果(注意下图并没有显示全连接层的节点连接)。
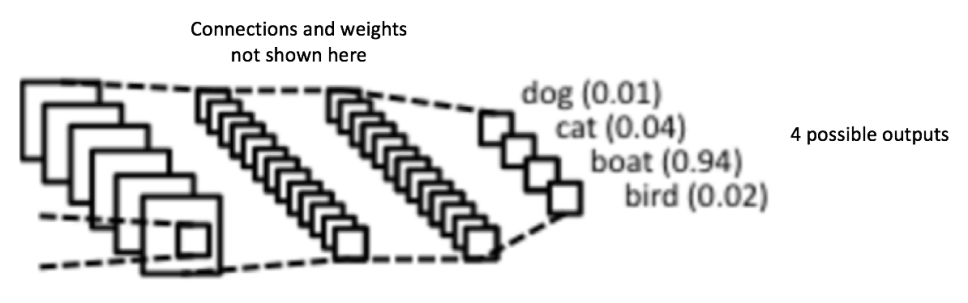
除了分类,添加一个全连接层也(一般)是学习这些特征的非线性组合的简单方法。从卷积和池化层得到的大多数特征可能对分类任务有效,但这些特征的组合可能会更好。
从全连接层得到的输出概率和为 1。这个可以在输出层使用 softmax 作为激活函数进行保证。softmax 函数输入一个任意大于 0 值的矢量,并把它们转换为零一之间的数值矢量,其和为一。
Use Backpropagation to Train whole network
正如上面讨论的,卷积 + 池化层的作用是从输入图像中提取特征,而全连接层的作用是分类器。
注意在下面的图中,因为输入的图像是船,对于船这一类的目标概率是 1,而其他三类的目标概率是 0,即
输入图像 = 船
-
目标矢量 = [0, 0, 1, 0]
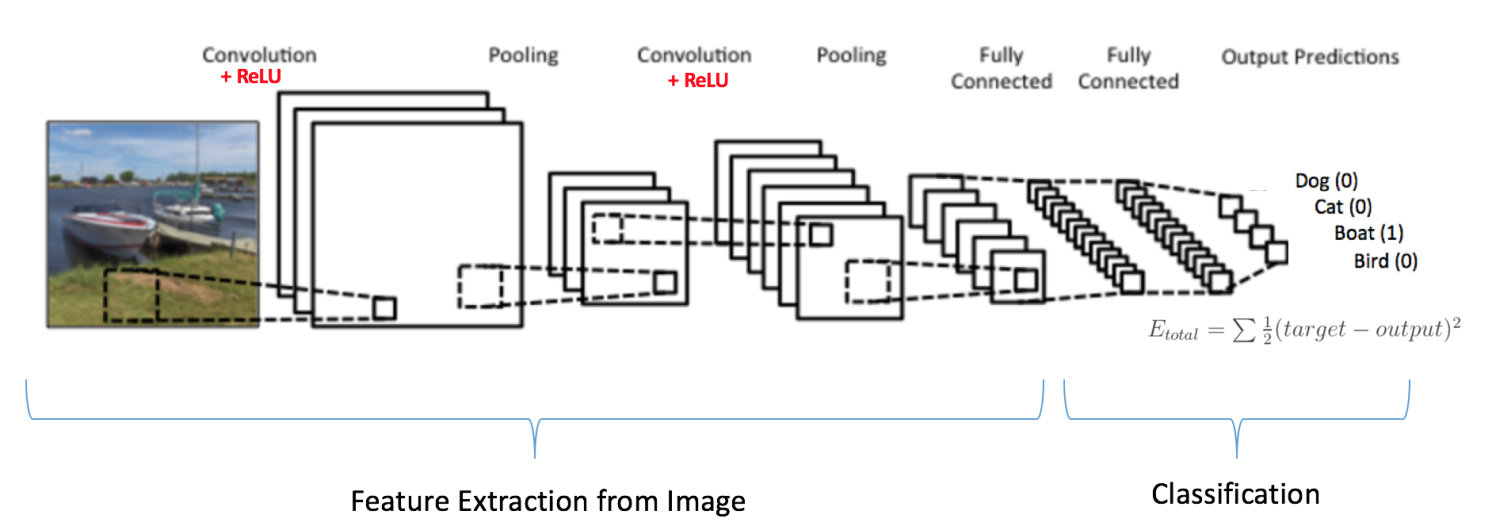
完整的卷积网络的训练过程可以总结如下:
- 第一步:我们初始化所有的滤波器,使用随机值设置参数/权重
- 第二步:网络接收一张训练图像作为输入,通过前向传播过程(卷积、ReLU 和池化操作,以及全连接层的前向传播),找到各个类的输出概率
- 我们假设船这张图像的输出概率是 [0.2, 0.4, 0.1, 0.3]
- 因为对于第一张训练样本的权重是随机分配的,输出的概率也是随机的
- 第三步:在输出层计算总误差(计算 4 类的和)
- Total Error = ∑ ½ (target probability – output probability) ²
- 第四步:使用反向传播算法,根据网络的权重计算误差的梯度,并使用梯度下降算法更新所有滤波器的值/权重以及参数的值,使输出误差最小化
- 权重的更新与它们对总误差的占比有关
- 当同样的图像再次作为输入,这时的输出概率可能会是 [0.1, 0.1, 0.7, 0.1],这就与目标矢量 [0, 0, 1, 0] 更接近了
- 这表明网络已经通过调节权重/滤波器,可以正确对这张特定图像的分类,这样输出的误差就减小了
- 像滤波器数量、滤波器大小、网络结构等这样的参数,在第一步前都是固定的,在训练过程中保持不变——仅仅是滤波器矩阵的值和连接权重在更新
- 第五步:对训练数据中所有的图像重复步骤 1 ~ 4
上面的这些步骤可以训练 ConvNet —— 这本质上意味着对于训练数据集中的图像,ConvNet 在更新了所有权重和参数后,已经优化为可以对这些图像进行正确分类。
当一张新的(未见过的)图像作为 ConvNet 的输入,网络将会再次进行前向传播过程,并输出各个类别的概率(对于新的图像,输出概率是使用已经在前面训练样本上优化分类的参数进行计算的)。如果我们的训练数据集非常的大,网络将会(有希望)对新的图像有很好的泛化,并把它们分到正确的类别中去。
注 1: 上面的步骤已经简化,也避免了数学详情,只为提供训练过程的直观内容。
注 2:在上面的例子中我们使用了两组卷积和池化层。然而请记住,这些操作可以在一个 ConvNet 中重复多次。实际上,现在有些表现最好的 ConvNet 拥有多达十几层的卷积和池化层!同时,每次卷积层后面不一定要有池化层。如下图所示,我们可以在池化操作前连续使用多个卷积 + ReLU 操作。还有,请注意 ConvNet 的各层在下图中是如何可视化的。

Visualization on CNN
一般而言,越多的卷积步骤,网络可以学到的识别特征就越复杂。比如,ConvNet 的图像分类可能在第一层从原始像素中检测出边缘,然后在第二层使用边缘检测简单的形状,接着使用这些形状检测更高级的特征,比如更高层的人脸。下面的图中展示了这些内容——我们使用卷积深度置信网络学习到的特征,这张图仅仅是用来证明上面的内容(这仅仅是一个例子:真正的卷积滤波器可能会检测到对我们毫无意义的物体)。
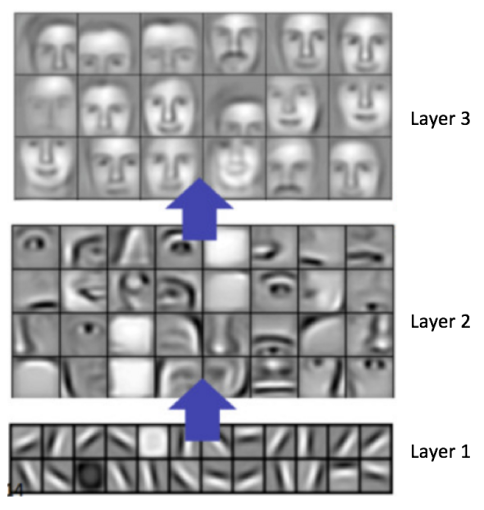
Adam Harley 创建了一个卷积神经网络的可视化结果,使用的是 MNIST 手写数字的训练集。我强烈建议使用它来理解 CNN 的工作原理。
我们可以在下图中看到网络是如何识别输入 「8」 的。注意下图中的可视化并没有单独展示 ReLU 操作。
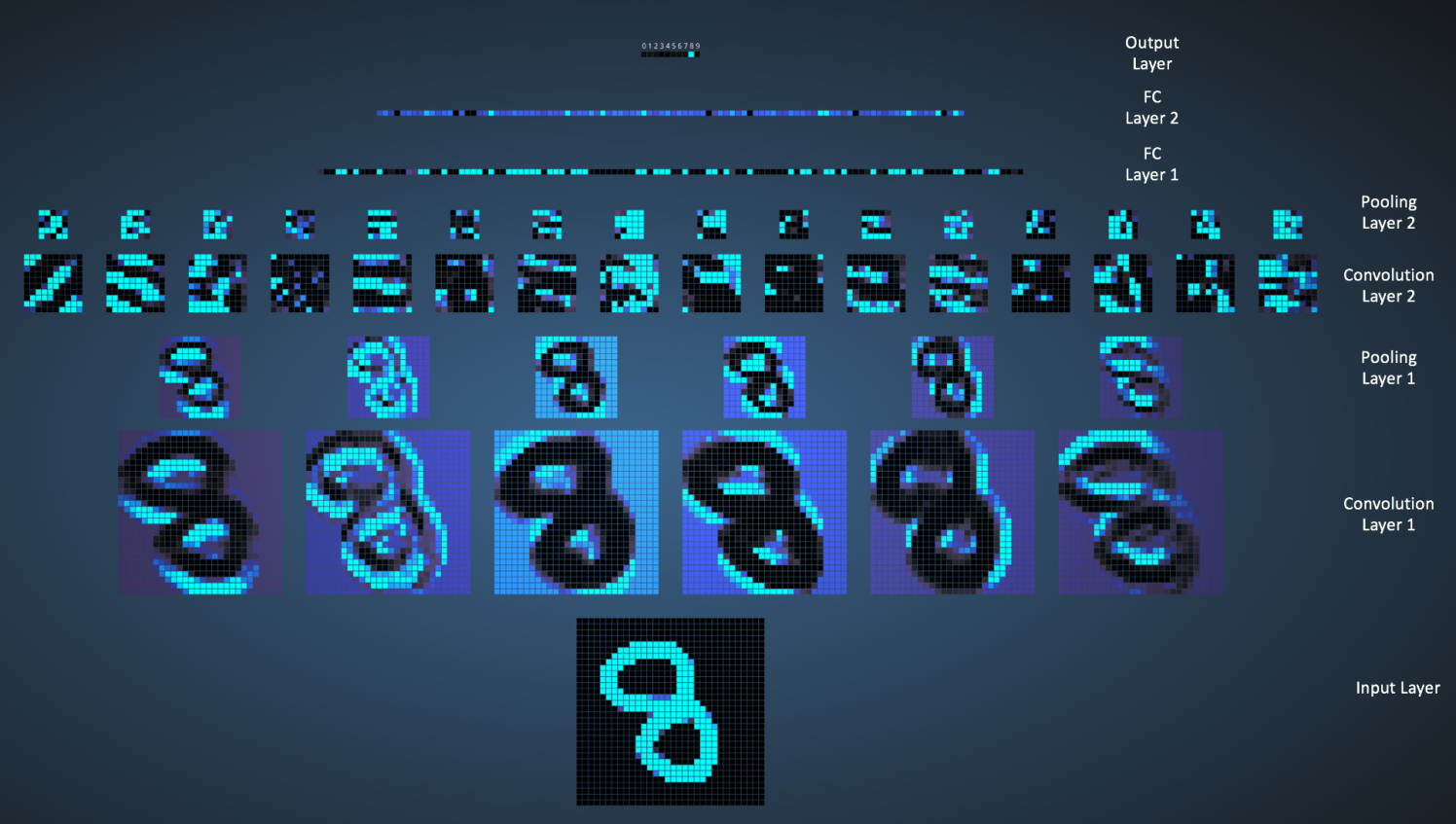
输入图像包含 1024 个像素(32 x 32 大小),第一个卷积层(卷积层 1)由六个独特的 5x5 (步长为 1)的滤波器组成。如图可见,使用六个不同的滤波器得到一个深度为六的特征图。
卷积层 1 后面是池化层 1,在卷积层 1 得到的六个特征图上分别进行 2x2 的最大池化(步长为 2)的操作。你可以在池化层上把鼠标移动到任意的像素上,观察在前面卷积层(如上图所示)得到的 4x4 的小格。你会发现 4x4 小格中的最大值(最亮)的像素将会进入到池化层。

池化层 1 后面的是六个 5x5 (步长为 1)的卷积滤波器,进行卷积操作。后面就是池化层 2,进行 2x2 的最大池化(步长为 2)的操作。这两层的概念和前面描述的一样。
接下来我们就到了三个全连接层。它们是:
- 第一个全连接层有 120 个神经元
- 第二层全连接层有 100 个神经元
- 第三个全连接层有 10 个神经元,对应 10 个数字——也就做输出层
注意在下图中,输出层中的 10 个节点的各个都与第二个全连接层的所有 100 个节点相连(因此叫做全连接)。
同时,注意在输出层那个唯一的亮的节点是如何对应于数字 “8” 的——这表明网络把我们的手写数字正确分类(越亮的节点表明从它得到的输出值越高,即,8 是所有数字中概率最高的)。
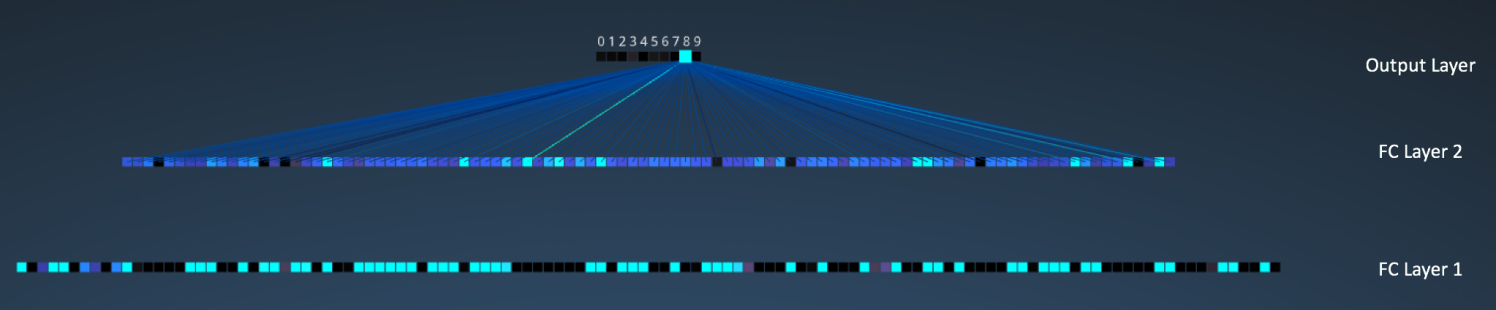
同样的 3D 可视化可以在这里看到。
Other ConvNet
卷积神经网络从上世纪 90 年代初期开始出现。我们上面提到的 LeNet 是早期卷积神经网络之一。其他有一定影响力的架构如下所示:
- LeNet (1990s): 本文已介绍。
- 1990s to 2012:在上世纪 90 年代后期至 2010 年初期,卷积神经网络进入孵化期。随着数据量和计算能力的逐渐发展,卷积神经网络可以处理的问题变得越来越有趣。
- AlexNet (2012) – 在 2012,Alex Krizhevsky (与其他人)发布了 AlexNet,它是比 LeNet 更深更宽的版本,并在 2012 年的 ImageNet 大规模视觉识别大赛(ImageNet Large Scale Visual Recognition Challenge,ILSVRC)中以巨大优势获胜。这对于以前的方法具有巨大的突破,当前 CNN 大范围的应用也是基于这个工作。
- ZF Net (2013) – ILSVRC 2013 的获胜者是来自 Matthew Zeiler 和 Rob Fergus 的卷积神经网络。它以 ZFNet (Zeiler & Fergus Net 的缩写)出名。它是在 AlexNet 架构超参数上进行调整得到的效果提升。
- GoogLeNet (2014) – ILSVRC 2014 的获胜者是来自于 Google 的 Szegedy等人的卷积神经网络。它的主要贡献在于使用了一个 Inception 模块,可以大量减少网络的参数个数(4M,AlexNet 有 60M 的参数)。
- VGGNet (2014) – 在 ILSVRC 2014 的领先者中有一个 VGGNet 的网络。它的主要贡献是展示了网络的深度(层数)对于性能具有很大的影响。
- ResNets (2015) – 残差网络是何凯明(和其他人)开发的,并赢得 ILSVRC 2015 的冠军。ResNets 是当前卷积神经网络中最好的模型,也是实践中使用 ConvNet 的默认选择(截至到 2016 年五月)。
- DenseNet (2016 八月) – 近来由 Gao Huang (和其他人)发表的,the Densely Connected Convolutional Network 的各层都直接于其他层以前向的方式连接。DenseNet 在五种竞争积累的目标识别基准任务中,比以前最好的架构有显著的提升。可以在这里看 Torch 实现。
CNN on TensorFlow
Tensorflow 在卷积和池化上有很强的灵活性。我们改如何处理边界?步长应该设多大?在这个实例里,我们会一直使用 vanilla 版本。我们的卷积网络选用步长(stride size)为 1,边距(padding size)为 0 的模板,保证输出和输入是同一个大小(严格卷积)。我们的池化选用简单传统的 $2 \times 2$ 大小的模板作为 max pooling(最大池化)。为了使代码更简洁,我们把这部分抽象成一个函数:
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides = [1, 1, 1, 1], padding = 'SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize = [1, 2, 2, 1], strides = [1, 2, 2, 1], padding = 'SAME')
Convolution Layer on TensorFlow
卷积操作是使用一个二维的卷积核在一个批处理的图片上进行不断扫描。具体操作就是将一个卷积和在每张图片上按照一个合适的尺寸在每个通道上面进行扫描。为了达到更好的卷积效率,需要在不同的通道和不同的卷积核之间进行权衡。
-
conv2d:任意的卷积核,能同时在不同的通道上面进行卷积操作。 -
depthwise_conv2d:卷积核能相互独立地在自己的通道上面进行卷积操作。 -
separable_conv2d:在纵深卷积depthwise filter之后进行逐点卷积separable filter。
注意:虽然这些操作被称之为「卷积」操作,但是严格地来说,他们只是互相关,因为卷积核没有做一个逆向的卷积过程。
卷积核的卷积过程是按照 strides 参数来确定的,比如 strides = [1, 1, 1, 1] 表示卷积核对每个像素点进行卷积,即在二维屏幕上面,两个轴方向的步长都是 1。strides = [1, 2, 2, 1]表示卷积核对每隔一个像素点进行卷积,即在二维屏幕上面,两个轴方向的步长都是 2。
如果我们暂不考虑通道这个因素,那么卷积操作的空间含义定义如下:如果输入数据是一个四维的 input ,数据维度是[batch, in_height, in_width, ...],卷积核也是一个四维的卷积核,数据维度是[filter_height, filter_width, ...],那么,对于输出数据的维度 shape(output),这取决于填充参数padding 的设置:
-
padding = 'SAME':向下取舍,仅适用于全尺寸操作,即输入数据维度和输出数据维度相同。out_height = ceil(float(in_height) / float(strides[1])) out_width = ceil(float(in_width) / float(strides[2])) -
padding = 'VALID':向上取舍,适用于部分窗口,即输入数据维度和输出数据维度不同。out_height = ceil(float(in_height - filter_height + 1) / float(strides[1])) out_width = ceil(float(in_width - filter_width + 1) / float(strides[2]))
output[b, i, j, :] =
sum_{di, dj} input[b, strides[1] * i + di, strides[2] * j + dj, ...] *
filter[di, dj, ...]
因为,input数据是一个四维的,每一个通道上面是一个向量input[b, i, j, :]。对于conv2d ,这些向量会被卷积核filter[di, dj, :, :]相乘而产生一个新的向量。对于depthwise_conv_2d,每个标量分量input[b, i , j, k]将在 k 个通道上面独立地被卷积核 filter[di, dj, k]进行卷积操作,然后把所有得到的向量进行连接组合成一个新的向量。
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)
这个函数的作用是对一个四维的输入数据 input 和四维的卷积核 filter 进行操作,然后对输入数据进行一个二维的卷积操作,最后得到卷积之后的结果。
给定的输入 tensor 的维度是 [batch, in_height, in_width, in_channels],卷积核 tensor 的维度是[filter_height, filter_width, in_channels, out_channels],具体卷积操作如下:
- 将卷积核的维度转换成一个二维的矩阵形状
[filter_height * filter_width* in_channels, output_channels] - 对于每个批处理的图片,我们将输入 tensor 转换成一个临时的数据维度
[batch, out_height, out_width, filter_height * filter_width * in_channels] - 对于每个批处理的图片,我们右乘以卷积核,得到最后的输出结果。
更加具体的表示细节为,如果采用默认的 NHWC data_format形式:
output[b, i, j, k] =
sum_{di, dj, q} input[b, strides[1] * i + di, strides[2] * j + dj, q] *
filter[di, dj, q, k]
所以我们注意到,必须要有strides[0] = strides[3] = 1。在大部分处理过程中,卷积核的水平移动步数和垂直移动步数是相同的,即strides = [1, stride, stride, 1]。
使用例子:
import numpy as np
import tensorflow as tf
input_data = tf.Variable(np.random.rand(10, 6, 6, 3), dtype = np.float32)
filter_data = tf.Variable(np.random.rand(2, 2, 3, 1), dtype = np.float32)
y = tf.nn.conv2d(input_data, filter_data, strides = [1, 1, 1, 1], padding = 'SAME')
with tf.Session() as sess:
init = tf.initialize_all_variables()
sess.run(init)
print(sess.run(y))
print(sess.run(tf.shape(y)))
输入参数:
-
input: 一个Tensor。数据类型必须是float32或者float64。 -
filter: 一个Tensor。数据类型必须是input相同。 -
strides: 一个长度是 4 的一维整数类型数组,每一维度对应的是 input 中每一维的对应移动步数,比如,strides[1]对应input[1]的移动步数。 -
padding: 一个字符串,取值为SAME或者VALID。 -
use_cudnn_on_gpu: 一个可选布尔值,默认情况下是True。 -
data_format:一个可选string,NHWC或者NCHW。默认是用NHWC。主要是规定了输入 tensor 和输出 tensor 的四维形式。如果使用NHWC,则数据以[batch, in_height, in_width, in_channels]存储;如果使用NCHW,则数据以[batch, in_channels, in_height, in_width]存储。 -
name: (可选)为这个操作取一个名字。
输出参数:
- 一个
Tensor,数据类型是input相同。
Pooling Layer on TensorFlow
池化操作是利用一个矩阵窗口在输入张量上进行扫描,并且将每个矩阵窗口中的值通过取最大值,平均值或者其他方法来减少元素个数。每个池化操作的矩阵窗口大小是由 ksize 来指定的,并且根据步长参数 strides 来决定移动步长。比如,如果 strides 中的值都是1,那么每个矩阵窗口都将被使用。如果 strides 中的值都是2,那么每一维度上的矩阵窗口都是每隔一个被使用。以此类推。
更具体的输出结果是:
output[i] = reduce( value[ strides * i: strides * i + ksize ] )
输出数据维度是:
shape(output) = (shape(value) - ksize + 1) / strides
其中,取舍方向取决于参数 padding :
-
padding = 'SAME': 向下取舍,仅适用于全尺寸操作,即输入数据维度和输出数据维度相同。 -
padding = 'VALID: 向上取舍,适用于部分窗口,即输入数据维度和输出数据维度不同。
tf.nn.avg_pool(value, ksize, strides, padding , data_format='NHWC', name=None)
这个函数的作用是计算池化区域中元素的平均值。
使用例子:
import numpy as np
import tensorflow as tf
input_data = tf.Variable( np.random.rand(10,6,6,3), dtype = np.float32 )
filter_data = tf.Variable( np.random.rand(2, 2, 3, 10), dtype = np.float32)
y = tf.nn.conv2d(input_data, filter_data, strides = [1, 1, 1, 1], padding = 'SAME')
output = tf.nn.avg_pool(value = y, ksize = [1, 2, 2, 1], strides = [1, 1, 1, 1], padding = 'SAME')
with tf.Session() as sess:
init = tf.initialize_all_variables()
sess.run(init)
print(sess.run(output))
print(sess.run(tf.shape(output)))
输入参数:
-
value: 一个四维的Tensor。数据维度是[batch, height, width, channels]。数据类型是float32,float64,qint8,quint8,qint32。 -
ksize: 一个长度不小于 4 的整型数组。每一位上面的值对应于输入数据张量中每一维的窗口对应值。 -
strides: 一个长度不小于 4 的整型数组。该参数指定滑动窗口在输入数据张量每一维上面的步长。 -
padding: 一个字符串,取值为SAME或者VALID。 -
data_format:一个可选string,NHWC或者NCHW。默认是用NHWC。主要是规定了输入 tensor 和输出 tensor 的四维形式。如果使用NHWC,则数据以[batch, in_height, in_width, in_channels]存储;如果使用NCHW,则数据以[batch, in_channels, in_height, in_width]存储。 -
name: (可选)为这个操作取一个名字。
输出参数:
- 一个Tensor,数据类型和value相同。
tf.nn.max_pool(value, ksize, strides, padding, data_format='NHWC', name=None)
这个函数的作用是计算 pooling 区域中元素的最大值。
tf.nn.max_pool_with_argmax(input, ksize, strides, padding, Targmax=None, name=None)
这个函数的作用是计算池化区域中元素的最大值和该最大值所在的位置。
因为在计算位置 argmax 的时候,我们将 input 铺平了进行计算,所以,如果 input = [b, y, x, c],那么索引位置是 `( ( b * height + y ) * width + x ) * channels + c
查看源码,该API只能在GPU环境下使用,所以我没有测试下面的使用例子,如果你可以测试,请告诉我程序是否可以运行。
源码展示:
REGISTER_KERNEL_BUILDER(Name("MaxPoolWithArgmax")
.Device(DEVICE_GPU)
.TypeConstraint<int64>("Targmax")
.TypeConstraint<float>("T"),
MaxPoolingWithArgmaxOp<Eigen::GpuDevice, float>);
REGISTER_KERNEL_BUILDER(Name("MaxPoolWithArgmax")
.Device(DEVICE_GPU)
.TypeConstraint<int64>("Targmax")
.TypeConstraint<Eigen::half>("T"),
MaxPoolingWithArgmaxOp<Eigen::GpuDevice, Eigen::half>);
使用例子:
import numpy as np
import tensorflow as tf
input_data = tf.Variable( np.random.rand(10,6,6,3), dtype = tf.float32 )
filter_data = tf.Variable( np.random.rand(2, 2, 3, 10), dtype = np.float32)
y = tf.nn.conv2d(input_data, filter_data, strides = [1, 1, 1, 1], padding = 'SAME')
output, argmax = tf.nn.max_pool_with_argmax(input = y, ksize = [1, 2, 2, 1], strides = [1, 1, 1, 1], padding = 'SAME')
with tf.Session() as sess:
init = tf.initialize_all_variables()
sess.run(init)
print(sess.run(output))
print(sess.run(tf.shape(output)))
输入参数:
-
input: 一个四维的Tensor。数据维度是[batch, height, width, channels]。数据类型是float32。 -
ksize: 一个长度不小于 4 的整型数组。每一位上面的值对应于输入数据张量中每一维的窗口对应值。 -
strides: 一个长度不小于 4 的整型数组。该参数指定滑动窗口在输入数据张量每一维上面的步长。 -
padding: 一个字符串,取值为SAME或者VALID。 -
Targmax: 一个可选的数据类型:tf.int32或者tf.int64。默认情况下是tf.int64。 -
name: (可选)为这个操作取一个名字。
输出参数:
一个元祖张量 (output, argmax):
-
output: 一个Tensor,数据类型是float32。表示池化区域的最大值。 -
argmax: 一个Tensor,数据类型是Targmax。数据维度是四维的。
Weight Initialization
所以,为了创建这个模型,我们需要创建大量的权重和偏置项,这个模型中的权重在初始化的时候应该加入少量的噪声来打破对称性以及避免 0 梯度。由于我们使用的是 ReLU 神经元,因此比较好的做法是用一个较小的正数来初始化偏置项,以避免神经元节点输出恒为 0 的问题(dead neurons)。为了不再建立模型的时候反复做初始化操作,我们定义两个函数用于初始化。
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides = [1, 1, 1, 1], padding = 'SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize = [1, 2, 2, 1], strides = [1, 2, 2, 1], padding = 'SAME')
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev = 0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape = shape)
return tf.Variable(initial)
第一层
接下来,我们开始实现第一层。它由一个卷积层接一个 max_pooling 最大池化层完成。卷积在每个 5x5 的 patch 中算出 32 个特征。卷积的权重张量形状是 [5, 5, 1, 32],前两个维度是 patch 的大小,接着是输入的通道数目,最后是输出的通道数目。而对于每一个输出通道都有一个对应的偏置量。
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
为了用这一层,我们把 x 变成一个 4d 的向量,其第 2、第 3 维对应图片的宽度、高度,最后一位代表图片的颜色通道(因为是灰度图,所以这里的通道数为 1,如果是 RBG 彩色图,则为 3)。
x_image = tf.reshape(x, [-1, 28, 28, 1])
之后,我们把 x_image 和权值向量进行卷积,加上偏置项,然后应用 ReLU 激活函数,最后进行 max pooling。
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
第二层
为了构建一个更深的网络,我们会把几个类似的层堆叠起来。第二层中,每个 5x5 的 patch 会得到 64 个特征。
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
密集连接层
现在,图片尺寸减小到 7x7,我们加入一个有 1024 个神经元的全连接层,用于处理整个图片。我们把池化层输出的张量 reshape 成一些向量,乘上权重矩阵,加上偏置,然后对其使用 ReLU。
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
Dropout
为了减少过拟合,我们在输出层之前加入dropout。我们用一个 placeholder 来代表一个神经元的输出在 dropout 中保持不变的概率。这样我们可以在训练过程中启用 dropout,在测试过程中关闭 dropout。 TensorFlow 的tf.nn.dropout 操作除了可以屏蔽神经元的输出外,还会自动处理神经元输出值的 scale。所以用 dropout 的时候可以不用考虑 scale。
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
输出层
最后我们添加一个 softmax 层,就像前面的单层 softmax regression 一样。
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
训练和评估模型
这个模型的效果如何呢?
为了进行训练和评估,我们使用与之前简单的单层 SoftMax 神经网络模型几乎相同的一套代码,只是我们会用更加复杂的 ADAM 优化器来做梯度最速下降,在 feed_dict 中加入额外的参数 keep_prob 来控制 dropout 比例。然后每 100 次迭代输出一次日志。
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
sess.run(tf.initialize_all_variables())
for i in range(20000):
batch = mnist.train.next_batch(50)
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={
x:batch[0], y_: batch[1], keep_prob: 1.0})
print "step %d, training accuracy %g"%(i, train_accuracy)
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print "test accuracy %g"%accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0})