Abstract
This article will discuss some problems in solar system again, including three-body motion, resonance of asteroids in the gap and chaotic tumbling of Hyperion.
Three-body motion
Problem 4.16
Three-body motion equations:
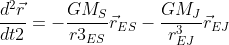

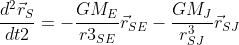
Use Euler-Cromer method to solve this equation,
1.when the value of
is real mass of Jupiter,both of the planets follow stable circular orbits.

if we add a time axis, it forms a 3D figure

2.When the value of
is 10 times of real mass of Jupiter

3D figures:

Jupiter has a little effect on Earth and Sun will move and its orbit is a small circle.
3.When the value of MJ is 100 times of real mass of Jupiter,

3D graph:

The orbit of Earth will precess obviously and forms beautiful pattern.Sun also distinctly moves along a circular orbit.
3.
When the value of MJ is 1000 times of real mass of Jupiter,

3D

They can't form a bound state Jupiter will be far away from Earth and Sun,leaving Earth rotating around Sun. If we decrease the initial speed of Jupiter, which can make Jupiter and Sun form a binary system. Let the initial speed of Jupiter become two-thirds of that value before.


The trajectory of Earth are chaotic.
2.Resonance
Similarly, we research the effect of Jupiter on asteroid whose period is a half of period of Jupiter

3D figure

Upper part and lower part of the trajectory of asteroid are somewhat thicker than other part of it, which demonstrates the resonance effect of Jupiter on asteroid.
3.Hyperion
Problem4.20
Equation
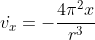
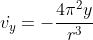
(xcos\theta+ysin\theta))
Use Euler-Cromer method to solve this equation,
When
its orbits is a circle.

Its motion is also regular and periodic.
If we plot the difference between two calculated results for
with different initial conditions


We can find that the absolute value of
is always smaller thean 0.01. It's not chaonic.Nevertheless,when

,#### it's orbit is an ellipse,

Its motion is weird and has no regulation that can be found.
Similarly,we plot the difference between two calculated results for
with different initial conditions


The absolute value of

is a larger and larger in general,thus the motion of this system can't be predicted.
Conclusions
•The tracjectory of one of three-body can be chaotic.
•The resonance effect of Jupiter on asteroid may be the reason that make that there is no asteriod in the 2/1 gap.
•In the problem of Hyperion, if the orbit of Hyperion is circular, its rotation is regular and periodic; if the orbit of Hyperion is elliptical, its rotation is chaotic and unpredicted