σ代数
令X是一个样本空间(sample space)Ω的所有子集(subsets)的集合的一个子集,那么集合X被称为σ代数(σ-algebra)又叫σ域(σ-field)。
它有以下几个性质:
(1)Φ∈X;(Φ为空集)
(2)若A∈X,则A的补集A^c∈X;
(3)若Ai∈X(i=1,2,…)则∪Ai∈X;
可测空间
Ω是任意集合,而X是把Ω中的极端情况去掉后又Ω的子集组成的集合,这样剩下的就是可以处理的集合,所以(Ω,X)称为可测空间(a measurable set)。X满足σ代数的三个性质,我们可以对X中的元素定义测度,故X的元素称为可测集(measurable set)。
测度空间
定义了测度的可测空间称为测度空间。
令(Ω,X)为一个可测空间,在X中定义一个方程ν称为测度(a measure)。
它满足以下条件:
(i )非负性:0≤ν≤∞
(ii )ν(空集)=0
(iii)如果Xi ∈X,其中Xi互不相交,则ν(∪Xi)=Σν(Xi)。
那么(Ω,X,ν)称为测度空间(measure space)。
勒贝格测度(Lebesgue Measure)
数学上,勒贝格测度是赋予欧几里得空间的子集一个长度、面积、或者体积的标准方法。它广泛应用于实分析,特别是用于定义勒贝格积分。可以赋予一个体积的集合被称为勒贝格可测;勒贝格可测集A的体积或者说测度记作λ(A)。
- 如果A是一个区间[a, b], 那么其勒贝格测度是区间长度b−a。 开区间(a, b)的长度与闭区间一样,因为两集合的差是零测集。
- 如果区间是[0,1],勒贝格测度L([0,1])是一个概率测度。
概率空间
如果ν(Ω)=1,则ν是概率测度,记为P。(Ω,X,P)称为概率空间。
这样,我们可以将P当做是对集合的一种测度,将集合和概率联系起来。
概率论研究的概率空间就是一个测度空间(Ω,X,P),其中P是定义在X中的测度,叫概率测度。集合Ω我们一般叫做样本空间,X中的元素叫可测集,但是我们更愿意叫做事件,而把X叫做事件域。任取X中元素A,它是Ω的子集,这时是一个事件,它的测度P(A)就是事件A的概率。可见这三元组(Ω,X,P)中的东西缺一不可。
对可测空间和测度空间的讨论
我们知道任一事件都是样本空间的子集,但样本空间的子集却不一定是事件。为了讨论方便,还是用一个比较好理解的现象作一个比喻。 假设研究人的性取向,这样样本空间X={男,女,不男不女},由于不男不女不好确定其性取向,这样在研究时就将这种情况排出,只研究男和女。或者说,样本空间是Ω={全体男人和女人},是个有限集,其对应的事件域取F={Ω的子集全体}完全可以,(Ω, F)就是可测空间。你说的性取向问题对应的F上的概率测度P是未知的,需要用统计方法确定。
更常见的做法是在(Ω,F,P)上定义一个随机变量,用统计方法确定随机变量的分布而不是P本身。例如任取ω∈Ω,定义X(ω)=0;若ω是和尚,X(ω)=1;若ω是尼姑,X(ω)=2;若ω是丈夫,X(ω)=3;若ω是妻子,X(ω)=4。
随机变量
定义一个随机变量X是一个可测的映射(a measurable map)X:Ω->R(该映射将集合映射成一个实数),使得Ω的任意一个元素ω(即事件)通过X(ω)赋予其一个实数。
这里,可测的意思是对于每个x,都有{ω:X(ω)≤x} ∈ A,这里的A是一个σ代数,其中的元素是可测的。
所以,概率是一个作用在集合中的测度。
分布函数
分布函数(Distribution Function,又称Cumulation Distribution Function),是一个映射Fx:R->[0,1]。
Fx(x)=P(X≤x),分布函数Fx将一个事件对应的随机变量映射为0到1的一个概率值。
应用举例
说了这么多,那么随机变量、概率分布具体是怎么和可测映射联系上的呢?我们以Bernoulli分布为例,介绍一下这其中的隐含关系。
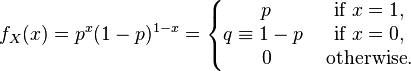
即当x=1时概率为p,当x=0时概率为1-p。
令样本空间Ω=[0,1],根据勒贝格测度,Pr([a,b])=b-a,其中0≤a<b≤1。
取一个固定的p∈(0,1),定义,当ω≤p时,X(ω)=1;当ω>p时,X(ω)=0。
于是,Pr(X=1) = Pr(ω≤p) = Pr([0,p]) = p; Pr(X=0)=1-p。
基于上面的介绍,我们可以发现,在日常的学习中,其实是省略了将集合映射到实数这一隐含的步骤的。
参考资料
转载请注明作者Jason Ding及其出处
Github博客主页(http://jasonding1354.github.io/)
CSDN博客(http://blog.csdn.net/jasonding1354)
简书主页(http://www.jianshu.com/users/2bd9b48f6ea8/latest_articles)