看了一本叫swift函数式编程的书，每一章就问题引入讨论了一下这个思想，我们来自己理解一下；首先上图，以及写一下传统做法；
首先我们按照书中的定义
typealias Position = CGPoint
typealias Distance = CGFloat
不懂typealias的请自行查阅；
我们总是这样做
-
图1所示，我们现在要表示一个未知点point是否在图中黑色圈圈内，很自然的，我们传入point参数，返回一个bool值，来解决这个问题，通常我们都会这样思考；
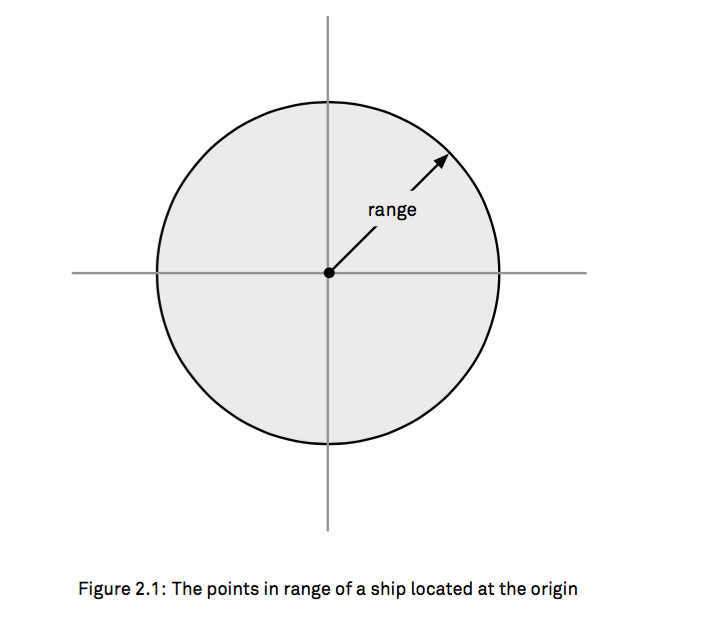inRange1
func inRange1(target: Position, range: Distance) -> Bool {
return sqrt(target.x * target.x + target.y * target.y) <= range
}
-
那么如果我们的圆心不在(0,0)点呢，需要做坐标系仿射变换（线性变换加上一个平移变换）对吧，或者理解仿射有点吃力，我们只做平移变换，就是说现在我们原点不是(0,0)了：
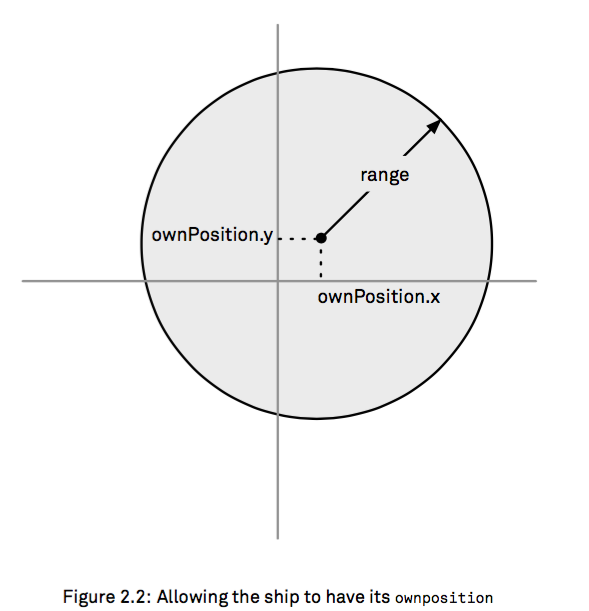inRange2
func inRange2(target: Position, ownPosition: Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(pow(dx, 2.0) + pow(dy, 2.0))
return targetDistance <= range
}
其实就是空间中的两个点得出一个相对距离，也很简单对吧，我们继续；
-
现在我们又有新需求了，我们要挖去中间的这个圆，因为我们的点现在要在这个环上运动了：
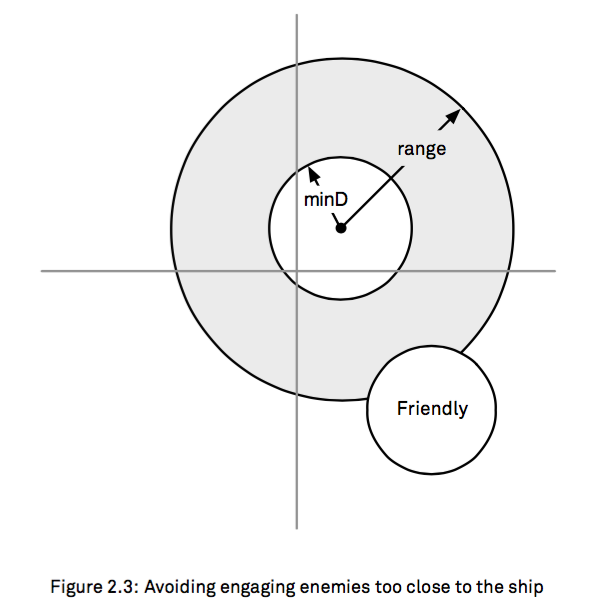inRange34
let minimumDistance: Distance = 2.0
func inRange3(target: Position, ownPosition: Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(pow(dx, 2.0) + pow(dy, 2.0))
return targetDistance <= range && targetDistance >= minimumDistance
}
就是需要我们挖去以原点为中心，半径为minimumDistance的圆，也还好；
- 我们还要考虑如果有一个圆，让这个圆在小圆环之外；
如上图中Friendly所示；
func inRange4(target: Position, ownPosition: Position, friendly:Position, range: Distance) -> Bool {
let dx = ownPosition.x - target.x
let dy = ownPosition.y - target.y
let targetDistance = sqrt(dx * dx + dy * dy)
let friendlyDx = friendly.x - target.x
let friendlyDy = friendly.y - target.y
let friendlyDistance = sqrt(pow(friendlyDx, 2.0) + pow(friendlyDy, 2.0))
return targetDistance <= range
&& targetDistance >= minimumDistance
&& friendlyDistance >= minimumDistance
}
我们还可以这样做
的确如书上所说，我做了好多重复的工作，而且从代码复制粘贴的情况来看，我似乎做了不少工作；太你太臃肿了，需要重构！
于是我们定义了这样一个关系，它是一个关系，也是一个值，作者说函数要当作是值来看待的；
typealias Region = (Position) -> Bool
理解起来也很容易：我是一个函数，我接受一个参数，你可以将Position的点让我来帮你验证，如果你通过我的验证，那你就是我要表达的Region，我会告诉你你的参数是不是我要的结果；
很顺畅对吧！接下来我们用它来写几个函数：
- inRange1重写
func circle(radius: Distance) -> Region {
return { position in
sqrt(pow(position.x, 2.0) + pow(position.y, 2.0)) <= radius //这不加 return 竟然也可以
}
}
- inRange2重写，平移变换圆
func shift(offset: Position, region: @escaping Region) -> Region {
return { position in
return region(Position(x: position.x + offset.x, y: position.y + offset.y))
}
}
- 写一个不是我范围的Region
func invert(region: @escaping Region) -> Region {
return { position in
!region(position)
}
}
- 来一个相交的区域
func intersection(region1: Region, region2: Region) -> Region {
return { point in
region1(point) && region2(point)
}
}
- 来一个并集的区域
func union(region1: Region, region2: Region) -> Region {
return { point in
region1(point) || region2(point)
}
}
- 再来一个差集
//函数表示在region中，而属于minusRegion的部分
func difference(region: Region, minusRegion: Region) -> Region {
return intersection(region1: region, region2: invert(region: minusRegion))
}
一时间发现把集合的性质写了一个遍，那如果把这个东西写成一个泛型，用的岂不是更多？
先不考虑，我们来重新写一下之前的那个inRange4吧！
最终inRange版本
func inRange(ownPosition: Position, target: Position, friendly: Position, range: Distance) -> Bool {
//表示灰色的圆环，顶点为(0,0)的圆环
let rangeRegion = difference(region: circle(radius: range), minusRegion: circle(radius: minimumDistance))
//发生了平移变换后的圆环
let targetRegion = shift(offset: ownPosition, region: rangeRegion)
//发生了平移变换后的朋友圈
let friendlyRegion = shift(offset: friendly, region: circle(radius: minimumDistance))
//最终结果为在目标圆环中，而不在朋友圈的区域
let resultRegion = difference(region: targetRegion, minusRegion: friendlyRegion)
return resultRegion(target)
}
结论
我不知道这过程中我做了什么，总的来说我貌似理解的更清晰了，改天再研究吧！你有什么想法，我们可以探讨一下啊！
