@[TOC](假设检验)
# 假设检验的概念
假设检验是统计推断的重要组成部分,分为参数假设检验与非参数假设检验。
参数假设检验是对总体分布函数中的未知参数提出某种假设,然后利用样本提供的信息对所提出的假设进行检验,根据检验的结果对所提出的假设作出拒绝或接受的判断。
非参数假设检验是对总体分布函数的形式或总体的性质提出某种假设所进行的检验。
## 原理及步骤
假设检验的特点就是采用逻辑上的反证法和依据统计上的小概率原理。小概率事件在单独一次的试验中基本上不会发生,可以不予考虑。在假设检验中,我们做出判断时所依据的逻辑是:如果在原假设正确的前提下,检验统计量的样本观测值的出现属于小概率事件,那么可以认为原假设不可信,从而否定它,转而接受备择假设。
一个完整的假设检验过程,包括以下几个步骤:
(1)**提出假设**;
(2)构造适当的检验统计量,并根据样本计算统计量的具体数值;
(3)规定显著性水平,建立检验规则;
(4)做出**判断**。
## 假设检验的种类
假设检验可分为正态分布检验、正态总体均值分布检验、非参数检验三类。
正态分布检验包括三类:JB检验、KS检验、Lilliefors检验,用于检验样本是否来自于一个正态分布总体。
正态总体均值检验检验分析方法和分析结果的准确度,考察系统误差对测试结果的影响。从统计意义上来说,各样本均值之差应在随机误差允许的范围之内。反之,如果不同样本的均值之差超过了允许的范围,这就说明除了随机误差之外,各均值之间还存在系统误差,使得各均值之间出现了显著性差异。
正态总体均值检验分为两种情况,
t检验是用小样本检验总体参数,特点是在均方差不知道的情况下,可以检验样本平均数的显著性,分为单侧检验与双侧检验。当为双样本检验时,在两样本t检验中要用到F检验。
从两研究总体中随机抽取样本,要对这两个样本进行比较的时候,首先要判断两总体方差是否相同,即方差齐性。若两总体方差相等,则直接用t检验,若不等,可采用t'检验或变量变换或秩和检验等方法。
Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。
上面所述的检验都是基于样本来自正态总体的假设,在实际工作中,有时并不明确知道样本是否来自正态总体,这就为假设检验带来难度。非参数检验方法,对样本是否来自正态总体不做严格的限制,而且计算简单。统计工具箱提供了符号检验和秩和检验两种非参数检验方法。
## 对假设检验问题做出判断可依据两种规则
(1)P值规则
所谓P值,实际上是检验统计量超过(大于或小于)具体样本观测值的概率。如果P值小于所给定的显著性水平,则认为原假设不太可能成立;如果P值大于所给定的标准,则认为没有充分的证据否定原假设。
(2)临界值规则
假设检验中,还有另外一种做出结论的方法:根据所提出的显著性水平标准(它是概率密度曲线的尾部面积)查表得到相应的检验统计量的数值,称作临界值,直接用检验统计量的观测值与临界值作比较,观测值落在临界值所划定的尾部(称之为拒绝域)内,便拒绝原假设;观测值落在临界值所划定的尾部之外(称之为不能拒绝域)的范围内,则认为拒绝原假设的证据不足。这种做出检验结论的方法,我们称之为临界值规则。
## 假设检验中的两类错误
第Ⅰ类错误 (type Ⅰ error)
又称弃真错误,当原假设为真时拒绝原假设。犯第Ⅰ类错误的概率通常记为α 。
第Ⅱ类错误(type Ⅱ error)
又称取伪错误,当原假设为假时没有拒绝原假设。犯第Ⅱ类错误的概率通常记为β。

在统计实践中,进行假设检验时一般先控制第Ⅰ类错误发生的概率,并确定犯第Ⅰ类错误的概率最大值,称为检验的显著性水平。在样本容量n不变的条件下,犯两类错误的概率常常呈现反向的变化,要使α和β 都同时减小,除非增加样本的容量。因此,统计学家奈曼与皮尔逊提出了一个原则:即在控制犯第一类错误的概率情况下,尽量使犯第二类错误的概率小。
在实际问题中,我们往往把要否定的陈述作为原假设,而把拟采纳的陈述本身作为备择假设,只对犯第一类错误的概率加以限制,而不考虑犯第二类错误的概率。
## 假设检验基本方法
### 检验形式
(1)双侧检验
双侧检验属于决策中的假设检验。也就是说,不论是拒绝H0,还是接受H1 ,都必需采取相应的行动措施。
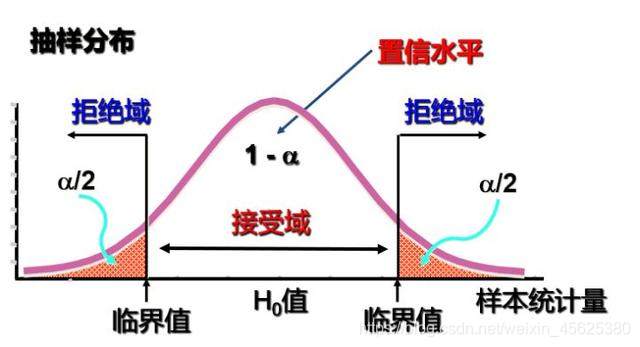
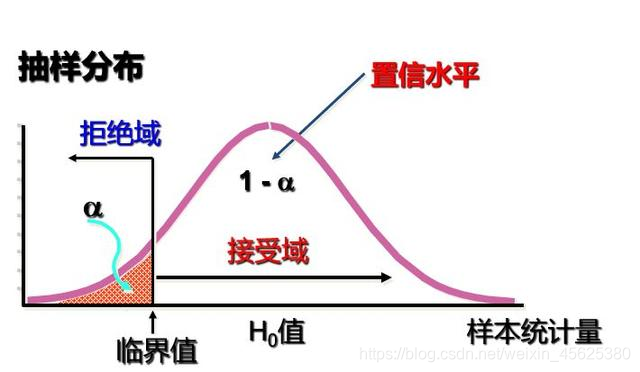
(2)单侧检验
单侧检验又可分两种形式:
a、检验研究中的假设
将所研究的假设作为备择假设H1,将认为研究结果是无效的说法或理论作为原假设H0。或者说,把希望(想要)证明的假设作为备择假设。再做这类假设检验时应先确立备择假设H1。
b、检验某项声明的有效性
将所作出的说明(声明)作为原假设,对该说明的质疑作为备择假设,在做这类单侧检验时,应先确立原假设H0。除非我们有证据表明“声明”无效,否则就应认为该“声明”是有效的。
### 单样本假设检验
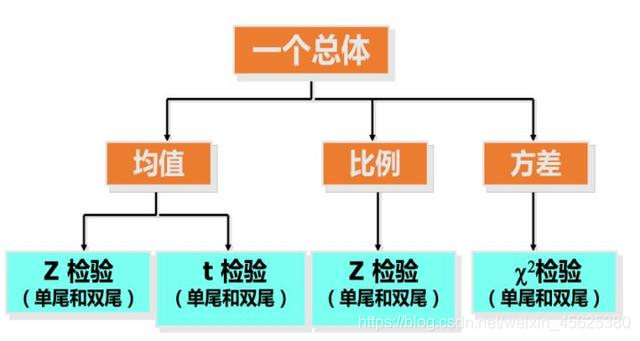
以均值为例进行如下分析分析,看适合哪种检验。
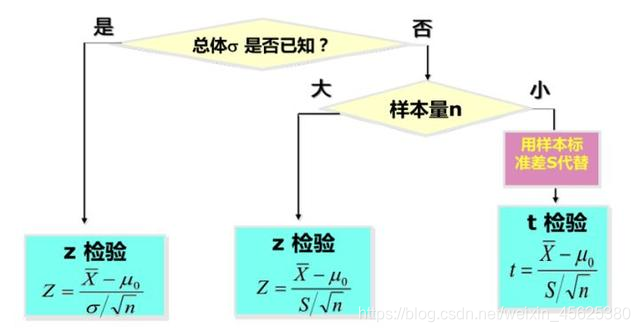
如果样本量足够大,那么Z检验和t检验将得出相同的结果。对于大样本,样本方差是对总体方差的较好估计,因此即使总体方差未知,我们也可以使用样本方差的Z检验。
同样,对于大样本,我们有很高的自由度。由于t分布接近正态分布,z分布和t分之间的差异可以忽略不计。
### 双样本假设检验
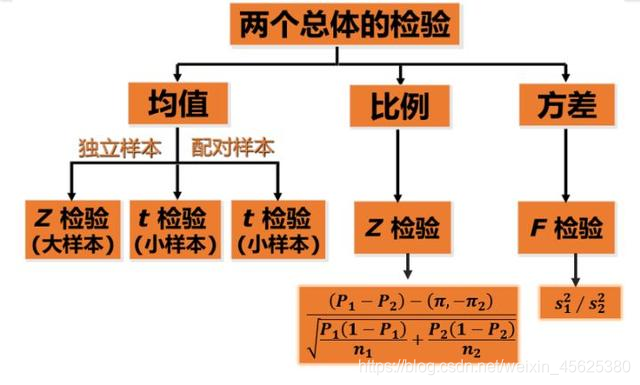
以均值差为例进行如下分析分析,看适合哪种检验。
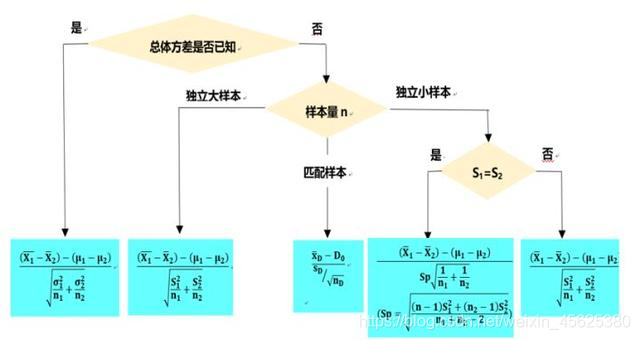
## 卡方检验、t检验和方差分析的区别
1、卡方检验 Chi-Square Test,关于什么是卡方检验可看这篇[结合日常生活的例子,了解什么是卡方检验](https://www.jianshu.com/p/807b2c2bfd9b)
卡方检验就是检验两个变量之间有没有相关性。
以运营为例:
卡方检验可以检验男性或者女性对线上买生鲜食品有没有区别;
不同城市级别的消费者对买SUV车有没有什么区别;
如果有显著区别的话,我们会考虑把这些变量放到模型或者分析里去。
2、t检验
亦称student t检验(Student's t test),主要用于样本含量较小(例如n < 30),总体标准差σ未知的正态分布。
T检验是用于两个样本(或样本与群体)平均值差异程度的检验方法。它是用T分布理论来推断差异发生的概率,从而判定两个平均数的差异是否显著。
3、方差分析
Analysis of Variance,简称ANOVA,又称“变异数分析”
从方差分析的目的来看,是要检验各个水平(因素中的内容)的均值μ1、μ2、…、μm是否相等(m为水平个数),而实现这个目的的手段是通过方差的比较(即考察各观察数据的差异)。通俗说,就是有没有变异。
#### 卡方检验和方差分析的区别:
1、二者的基本思想不同
方差分析基本思想:变异分解,总变异=随机变异+处理因素导致的变异,又可以分解为总变异=组内变异+组间变异,F=组间变异/组内变异,F的值越大,处理因素的影响越大。
卡方检验基本思想:以卡方分布为基础,计算观察值和期望值之间的偏离程度。
2、适用的前提条件不同
方差分析:数据具有独立性、正态性、方差齐性。
卡方检验:最小期望频数均大于1;至少4/5的单元格期望频数大于5;计算时如果单元格期望频数小于5要和其他种类合并;样本观察值量超过50。
3、适用的场景不同
方差分析:均数间的多重比较(全部两两比较)、各组均数的精细比较(可以指定要比较的两个组,通过设定系数)、组间均数的趋势检验(为了利用分组变量中体现出的次序信息,目的不是为了拟合线性或非线性的模型,而是希望知道因素的水平改变时均数的变化趋势)。
卡方检验:单样本卡方检验、两样本卡方检验、两分类变量间关联程度的度量、Kappa一致性检验、Mcnemar 配对卡方检验、分层卡方检验。
#### 卡方检验和t检验的区别:
卡方检验和T检验的前提条件(原假设)是对立的:
卡方检验:假设没有相关性
T检验:假设没有差异(相等)
卡方检验主要检验几个变量之间的独立性,也就是有没有关联,而t检验更多的检验显著性,也就是几组数据到底一不一样,即相关性和显著性的区别。