A题“洗个热水澡”是一道涉及热传导的连续性问题,用到了牛顿冷却定律、N-S方程等公式定理进行模型的建立,同时利用CFD等软件进行流体的模拟,降低了编程建模的难度。
为了方便讨论模型,这篇论文中做了一些处理
-
做出一些假设,让我们的关注点集中在问题上面
- 浴缸水是不可压缩的非牛顿流体,非牛顿流体是应用N-S方程模拟洗澡水流动的基础
洗澡水、空气、浴缸等是保持稳定的,如空气密度的变化对于模型的影响可以忽略,浴缸和水的比热的变化也是可以忽略的
整个系统中没有内能源对体系输入能量
我们忽略辐射能的损失,根据波尔兹曼辐射率,当温度较低时,物体的辐射能很小可以忽略不计
加入的热水温度是保持恒定的
做一些标记,方便分析模型
将模型分为两步,一步模型是持续地放水,另一步模型是间断地放水
分析一些影响因素:如浴缸的形状和容量,人在洗澡时的动作等
一些标记

goal
在我们的模型中,我们有三个目标:
- 尽可能保持温度恒定
- 使温度保持在初始条件下
- 减少水的浪费
模型一:持续的加水
1.首先假设浴缸的形状是一个长方体:

由于流体是稳定连续流进流出的,因此我们提出一个连续性方程:
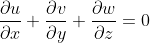
由于流体不可压缩,应用N-S方程:
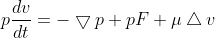
由于系统没有外力作用,因此将上述方程转化为

同时我们还要考虑到热量在体系中传输的影响,因此再加上热量传输微分方程:
- 对于不可压缩流体来说有:
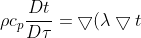+q_v + \phi) - 对于流体高速流动或者粘性很大的流体来说,我们需要考虑\phi,在本模型中,我们可以简化为:
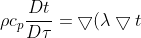)
即:
=\lambda(\frac{\partial ^2 t}{\partial x^2}+\frac{\partial ^2 t}{\partial y^2}+\frac{\partial ^2t}{\partial z^2}))
边界情况:
流入的水的温度是
水面和空气之间会发生热量交换,根据牛顿冷却定律(牛顿冷却定律(Newton's law of cooling):温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。当物体表面与周围存在温度差时,单位时间从单位面积散失的热量与温度差成正比,比例系数称为热传递系数。):
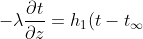)
其边界条件为:
同时浴缸壁也会与周围环境交换热量,因此有:
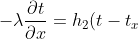)
边界条件为: