做完这题觉得必须得来个解题报告了,这题的动态规划有点酸爽啊~
问题如下:
编辑距离,又称Levenshtein距离,是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
以上的问题可以用众所周知的动态规划解决,现在的问题是,如果新加入一种编辑操作:交换相邻的两个字符;求两个字符串之间的编辑距离。
输入为2个字符串(长度小于1000),输出为两个串的编辑距离。
L氏距离(Levenshtein Distance)
基础的编辑距离只有3种原子操作:插入1个字符,删除1个字符,更改1个字符.且3种操作的代价均为1.
设串A为a1 a2 ... am, 串B为b1 b2 ... bn
将串A经过n个操作x1 - x2 - ... - xn,使之变成串B,且该操作序列为最优操作(代价之和最小)的一种,则2个串的L氏距离即为该序列代价之和。通常3个操作的代价都为1,也有可能按某种方案加权(即3种操作的代价不一致,导致更复杂的情况,这里只讨论都是1的).

这种编辑距离可以很直观地用DP得到:(同时网络上的中文资料大部分都为这种距离)
用C[i,j]表示a1 a2 ... ai到b1 b2 ... bj的距离,则有以下状态转移方程:


上面的转移方程是很直观的,有人会问这样每次只考虑对于两个串的最后一个元素的操作是否会错过最优解,这个可以通过归纳法证明此种求解方法得到的就是最优解。
每个C[i,j]都由下标严格小于i和j的元素C[i-1,j-1]/C[i-1,j]/C[i,j-1]决定。
算法流程即为从左到右,从上到下遍历矩阵C,最后的整个串的L氏距离值为C[m,n]。
L氏距离有一些性质,这里不具体展开了...(-. -!)
D氏距离
<b>1.引子</b>
上面讲了那么多,然而并没有什么卵用。
题目中增加了transposition操作,可以交换2个相邻元素,并且这个操作的代价也是1.那么问题来了,原先的状态转移方程需要如果改变呢?
最开始我的思路是这样的,直觉+观察发现对于原先方程中的第三个式子,在某些条件下,若用交换代替原来的操作,可以使总代价减少1:
当ai != bj 且 ai-1 != bj-1时:可能通过subs(修改最后一个元素),从而C[i,j]可能是C[i-1,j-1]+1(也可能是另外2个操作)
若同时ai-1 = bj且ai = bj-1,则只需交换最后2个元素即可,则该操作代价应比subs少1,从而可排除此轮subs的操作在最优操作序列中的可能性。
<b>2. 2种镜像操作</b>
这里观察发现的交换实际上只是相邻2个字符交换的情况,推广到一般情况,很可能会有如下的操作:
- 交换2个相邻字符,并在其之间插入字符。
- 删除某2个不相邻字符之间的所有字符,并使之交换。
这2种操作很有可能比原来的代价要低。
<b>3. 严格编辑距离与D氏距离</b>
另外这里还需要引入另一个概念,所谓严格编辑距离,这个的意思是每次操作只能改变串A的一个位置(最后一个位置),严格定义见wiki:optimal string alignment[citation needed] (sometimes called the restricted edit distance[citation needed]
), 我个人理解就是不能往中间插入,每次只能更改串的最后一个字符(或者加入新字符或者删改原串中的最后一个字符)。
这里给了一个例子,AC 和 CBA 的距离,若是严格编辑距离为4,则操作为:AC - CA - CB - CBA(或其他);若是D氏距离则为3,操作为AC - CA - CBA,对于删除同理。
本题中的“距离”应该指的是后者。
<b>4. 最优子结构性质</b>
L氏距离的DP求解有个性质,就是某个步骤中的操作一旦被认为是最优的,则后续的操作不会再对前面的串再做更改(再更改会使总代价变高)。即存在最优子结构。
那D氏距离是否存在最优子结构呢?
实际上有个结论,当trans的代价大于等于插入和删除代价和一半时,trans交换过的元素不会再被更改(Wiki - there always exists an optimal sequence of edit operations, where once-transposed letters are never modified afterwards. (This holds as long as the cost of a transposition,
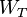

) )
<b>5. 状态转移方程</b>
结合上面几点,开了开脑洞,我想出了这样的方程


其中,k1和k2一开始我的想法是只要能满足的交换条件的都去遍历一遍,实际上只需要计算距离当前i,j最近的一次"交叉相等"即可.(即满足交叉相等的2个下标尽可能大)
由于交换需要的条件是相邻,因此,该操作需要先删除串A中本来存在k1 .. i之间的所有元素,并且在交换k1 .. i之后插入所有B中相应的元素,因此就有后面那堆i,k1,j,k2的运算。
为什么是最“近”呢?
假设存在一个比较“远”的
k3/k4满足交换条件,即A[k3] = B[j] & A[i] = B[k4],且有 k3 + k4 < k1 + k2。这里就考虑A中的元素
A[k3+1 .. k1-1]和 B中的 B[k4+1 .. k2-1],相信你已经想到了,比较近的方案中,这些元素都寻求最优的操作。而较远的方案中,采取的是删除A中元素,插入B中元素,则必定大于或等于最优操作。因此只需要选择最“近”的方案即可。
<b>6. 相信到这里就已经可以写出O(N*M)的算法了</b>
其中,Wiki的算法最为简洁(是Wiki页面上的算法2)。
D-L距离