Linear Discriminant Analysis 线性判别分析因最早由Fisher提出又称为“Fisher判别分析”。LDA是一种经典的线性分类学习方法，同时，因为其可以将样本投影到低维的空间，又常被当作监督降维的手段。
LDA的基本思想是：给定两类样本集，将其投影到一条直线上去，使同类样本的投影点尽可能的接近，不同类样本的投影点尽可能远离。
这里就涉及到两个因素：
- 使同类样本的投影点尽可能的接近，也就是说使同类样本的投影点的方差尽可能的小。
- 使不同类样本的投影点尽可能远离，也就是说使不同类样本投影点的中心点的距离尽可能的大。
201104212324555025.jpg
上图是一个二维示意图，我们明显可以看出来选择右边的投影线段比左边的好很多。
我们先考虑简单一点的情形，把数据映射到一维。
我们再用数学语言重新描述一下我们的问题：
对于归属于两类的样本点,找到一个向量w，使得经过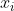
转换后的投影点能够自动的分成两类。
接下来我们来看看如何找到这个w。
这其实是一个线性变化，投影后的中心点也就是中心点的投影点。
它是两个向量的外积，又被称为类间散度矩阵(between-class scatter matrix)，我们称其为Sb。
我们再考虑第一个因素，使投影后同类样本的方差最小。投影后的样本方差如下：我们看其中间的部分
那么，此时我们的目标就变成了找出一个w使J(w)最大。
再考虑，w其实代表的是一个方向，它本身的大小是无所谓的，则我们总是可以缩放w使得