**分析一个算法的好坏,时间复杂度是一个很重要的标准。那么什么是时间复杂度呢?**
举个栗子,
A和B要从同一个起点X出发,去目的地Y,从X到Y有很多种方式。A选择步行过去,B选择打车过去。那么通常情况下,B会比A先到目的地Y。
这个例子中,从X到Y就是程序需要实现的功能,而步行和打车相当于两种不同的算法,但是这两种算法实现的功能是一样的。显然这两种不同的算法为了实现同一个功能花费的时间是不同的。
在计算机科学中,时间复杂度,就是这样一个定性地描述该算法运行时间的指标。时间复杂度通常用大写的‘O’表示。
常见的算法时间复杂度有(从小到大排):
O(1)常数阶 <O(logn)对数阶 <O(n)线性阶 <O(nlogn)< O(n^2) <O(n^3)< O(2^n)< O(n!)
计算时间复杂度可分为递归和非递归两种:
举一个简单的例子:计算斐波那契数列 f(n) = f(n-1) + f(n-2) (n<=45)
很多人第一眼看到这个问题,觉得用递归十分方便,便毫不犹豫的用了递归,其实当我们计算一下这个问题的时间复杂度之后,我们会发现使用递归时存在一个很大的问题。
如果我们使用递归的方式,那么我们设进入一次递归为一个基本操作,进行一个基本操作为一个单位的时间1。
那么当计算f(3)时候,如下图:
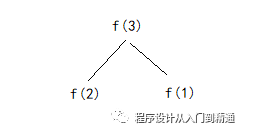
我们消耗的时间为T(3)=T(2)+T(1)+1,加1是因为除了f(2)和f(1)消耗的时间外,计算f(3)进入递归也消耗了1单位时间。
故运算完f(n)所花费时间为,T(n) = T(n-1) + T(n-2) + 1
变形,(T(n) + 1) = (T(n-1) + 1) + (T(n-2) + 1)
令B(n) = T(n) + 1,
得B(n) = B(n-1) + B(n-2)
可见B(n)也是一个斐波那契数列,
所以时间复杂度T(n) = B(n) - 1,实际消耗如下图,

就这样,最顶层消耗由f(n-1)和f(n-2)的消耗时间T(n-1)和T(n-2)组成,每层都是一分为二,二分为四,因为n的范围是n<=45,当n达到45时,上述计算的节点达到恐怖的(2^44)这个级别(系数可忽略不计)。这是不可想象的,因为递归的过程中进行了大量的无用的重复运算。
如果我们采用非递归的方法递推的话,十分简单,时间复杂度为O(n)。样例代码如下:
for(int i = 3; i <= n; i++)
{
f[i] = f[i-1] + f[i-2]
}
消耗节点如下:

最终只执行了(n)这个级别的次数。
所以在解题码代码之前,进行时间复杂度的分析是非常重要的。