在之前的对行星运动的讨论中,我们只关注两体间的作用力对轨道造成的影响,这一次我们考虑三个物体间的相互作用力对物体运动轨道的影响,即三体问题。
In physics and classical mechanics, the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then determining the motions of the three bodies, in accordance with the laws of classical mechanics (Newton's laws of motion and of universal gravitation). The three-body problem is a special case of the n-body problem.

理论求解
木星与地球之间的相互作用力为:


将地球与木星之间的相互作用力投影到x轴:
因此,x方向上的速度变化为:
,
同时我们在这里可以做一个简化处理:
其中,太阳和木星的质量已给出。
具体算法
在每次迭代中面积算地球,木星的位置和速度
-
计算地球、木星和太阳之间的距离
=\sqrt{x_e(i)2+y_e(i)2}\ r_j(i)=\sqrt{x_j(i)2+y_j(i)2})
计算地球的实时速度
=v_{e,x}(i)-\frac{4\pi2x_e(i)}{r_e(i)3}\Delta t-\frac{4\pi2(M_J/M_S)[x_e(i)-x_j(i)]}{r_{EJ}(i)3})计算木星的实时速度
=v_{j,x}(i)-\frac{4\pi2x_j(i)}{r_j(i)3}\Delta t-\frac{4\pi2(M_E/M_S)[x_j(i)-x_e(i)]}{r_{EJ}(i)3})-
使用欧勒法计算地球和木星的位置
木星位置的计算方法和上面类似
将新位置的点绘制出来
进行下一次迭代
具体代码
# -*- coding: utf-8 -*-
# author:Ricardo #
# three body simulation #
import math
import numpy as np
import matplotlib.pyplot as pl
class PlanetOrbit:
def __init__(self,time_step=0.001,init_ex=1.00,init_ey=0,init_jx=5.20,init_jy=0,init_evx=0,
init_evy=2*math.pi,init_jvx=0,init_jvy=0.872*math.pi,total_time=3.65,M_J=1900000,M_S=2000000,M_E=6.0):
self.Kep = 4*pow(math.pi,2)
self.dt = time_step
self.re = [] #distance between sun and earth
self.rj = [] #distance between sun and jupiter
self.r_ej = [] #distance between earth and jupiter
self.e_x = [init_ex] #the x position of earth
self.e_y = [init_ey] #the y position of earth
self.j_x = [init_jx] #the x position of jupiter
self.j_y = [init_jy] #the y position of jupiter
self.v_ex = [init_evx] #the x-speed of earth
self.v_ey = [init_evy] #the y-speed of earth
self.v_jx = [init_jvx] #the x-speed of jupiter
self.v_jy = [init_jvy] #the y-speed of jupiter
self.t = total_time
self.parameter_M_JS=M_J/M_S #the value of M_J/M_S
self.parameter_M_ES=M_E/M_S #the value of M_E/M_S
def run(self):
loop = True
i=0
while(loop):
# calculate the distances among Earth,Jupiter and Sun:
self.re.append(pow((pow(self.e_x[i],2)+pow(self.e_y[i],2)),0.5))
self.rj.append(pow((pow(self.j_x[i],2)+pow(self.j_y[i],2)),0.5))
self.r_ej.append(pow((pow((self.e_x[i]-self.j_x[i]),2)+pow((self.e_y[i]-self.j_y[i]),2)),0.5))
# Compute the new velocity of Earth
self.v_ex.append(self.v_ex[i]-(self.Kep*self.e_x[i]/pow(self.re[i],3))*self.dt-(self.Kep*self.parameter_M_JS*(self.e_x[i]-self.j_x[i]))/pow(self.r_ej[i],3)*self.dt)
self.v_ey.append(self.v_ey[i]-(self.Kep*self.e_y[i]/pow(self.re[i],3))*self.dt-(self.Kep*self.parameter_M_JS*(self.e_y[i]-self.j_y[i]))/pow(self.r_ej[i],3)*self.dt)
# Compute the new velocity of Jupiter
self.v_jx.append(self.v_jx[i]-(self.Kep*self.j_x[i]/pow(self.rj[i],3))*self.dt-(self.Kep*self.parameter_M_ES*(self.j_x[i]-self.e_x[i]))/pow(self.r_ej[i],3)*self.dt)
self.v_jy.append(self.v_jy[i]-(self.Kep*self.j_y[i]/pow(self.rj[i],3))*self.dt-(self.Kep*self.parameter_M_ES*(self.j_y[i]-self.e_y[i]))/pow(self.r_ej[i],3)*self.dt)
# calculate the new position of Earth and Jupiter
# Earth
self.e_x.append(self.e_x[i]+self.v_ex[i+1]*self.dt)
self.e_y.append(self.e_y[i]+self.v_ey[i+1]*self.dt)
# Jupiter
self.j_x.append(self.j_x[i]+self.v_jx[i+1]*self.dt)
self.j_y.append(self.j_y[i]+self.v_jy[i+1]*self.dt)
# i increase
i += 1
if (i>=(self.t/self.dt-1)):
loop = False
def DrawOrbit(self):
pl.plot(self.e_x,self.e_y,'.',markersize=2,label="Mass of Jupiter = M_J")
pl.plot(self.j_x,self.j_y,'.',markersize=2)
pl.title('3-body simulation Earth plus Jupiter')
pl.xlabel('x(AU)')
pl.ylabel('y(AU)')
pl.axis('equal' )
pl.legend()
pl.show()
结果分析

可以发现,木星的质量对地球轨道几乎没有影响,即使将它的质量增大到原来的十倍,也看不出有什么影响

当木星质量增大到原来的1000倍时,地球轨道就受到了严重的影响...
但是上面的计算还没有考虑太阳受到它们的影响时轨道的变化...
因此,接下来我将太阳的运动也一起放进去计算....

画出了地球的轨道2333
关于Hyperion运动轨道的讨论
Hyperion, also known as Saturn VII (7), is a moon of Saturn discovered by William Cranch Bond, George Phillips Bond and William Lassell in 1848. It is distinguished by its irregular shape, its chaotic rotation, and its unexplained sponge-like appearance. It was the first non-round moon to be discovered.
The Voyager 2 images and subsequent ground-based photometry indicated that Hyperion's rotation is chaotic, that is, its axis of rotation wobbles so much that its orientation in space is unpredictable. Its Lyapunov time is around 30 days.[16] Hyperion, together with Pluto's moons Nix and Hydra,[17][18] is among only a few moons in the Solar System known to rotate chaotically, although it is expected to be common in binary asteroids.[19] It is also the only regular planetary natural satellite in the Solar System known not to be tidally locked.

理论求解
可以将Hyperion看作由一根刚性杆连接的两个小球1和2,小球1和小球2分别受到土星的引力作用,小球1受到的引力为:
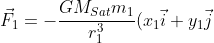\newline M_{Sat}:the\ of\ Saturn \newline r_1:the\ distance\ from\ Saturn\ to\ m_1)
小球2 的受力情况与上面类似。
因此,小球1受到的力矩为:
小球2受到的力矩也是如此。
因此Hyperion角速度的变化如下所示:
其中:
将上述式子标量化之后得到:
(x_ccos\theta+y_csin\theta)\newline \newline r_c:the\ distance\ from\ the\ center\ of\ mass\ to\ Saturn)

模拟结果分析

为了简化计算,我们令Hyperion的质心离土星的距离为1HU(which might be called "Hyperion unit"),环绕周期为1"Hyperion-year",时间步伐为0.0001Hyperion-year

当将Hyperion的初始速度稍微增大时,就出现了混沌现象。

继续增大其初始速度,Hyperion的运动将更不规律。