本文来自麻省理工ECE教授Scott Aaronson的教学讲义。和我们大多数人学的物理课不同,这门课是量子计算,从另外一个角度来理解量子力学。当时读到这篇文章觉得很有意思,便打算翻译过来和大家一起分享。由于本人学识浅薄,翻译中若有错误欢迎大家指正。另外这是课堂讲义,口语化的文字很难翻译,一些我觉得不重要的内容就略去不翻或者意译了。
量子力学的教学,有两种方法。第一种方法是如今大多数物理学家采用的,以历史发展的顺序,先从经典力学讲到电动力学,解一大堆微分方程,然后告诉你黑体辐射悖论和那些奇奇怪怪的实验结果,这些导致了物理学的危机。然后你会学习那些物理学家在1900和1926年之间提出来的各种复杂想法来解救这个危机。幸运的话,经过多年的学习你最终接触到这个中心概念:世界不是由概率(probabilities)描述的,而是由一些叫做振幅(amplitudes)的数字描述的。概率是非负的,而振幅可正可负,甚至可以是复数。
如今是量子信息时代,所有物理学家都用这种方法来学习量子力学的话就有点可笑。那些受过高等教育的人只不过记住了这些话:“光具有波粒二象性”,“薛定谔的猫不知是死是活除非你打开箱子瞧一瞧”,“你可以知道位置(position)或动量(momentum),但是不能两个都知道”,“一个粒子知道另一个粒子的自旋即使距离很远” 等等。但是我们根本不能理解这些,除非我们痛苦地学习好多年。
第二种教学方法抛弃了量子力学的历史发展过程,直接跳到其核心概念,也就是一个允许负号的概率理论。一旦你理解了这个理论,你就能品尝物理,就能计算任意原子的谱带。这个第二种方法就是我所采用的。
那么什么是量子力学?尽管是由物理学家发现的,量子力学和电磁学及广义相对论相比,并不是同一类的物理学。从科学的继承性来看,生物学来自化学,化学来自物理,物理来自数学,而量子力学位于物理和数学之间。量子力学就像是个操作系统,而其他物理理论就像是计算机应用程序(除了广义相对论没能兼容这个系统)。甚至可以用一个词来形容把一个物理理论安装到这个操作系统上:“量子化”。
如果量子力学不是关于一般的物理概念(物质,能量,波,粒子),那么它是关于什么的?在我看来,量子力学是关于信息,概率,观察 以及它们之间的联系的理论。
我的观点是,如果你研究概率论,那么最后肯定会触及量子力学。所以我们不如把概率这个概念扩大化,让概率也可以取负数。如果早这么做的话,19世纪的数学家就可以发明量子力学了,根本就不需要实验。
Scott: 在我看来,这说明了实验的重要性。很多时候我们做实验是因为我们不够聪明,必须通过分析实验结果来提出理论。
在这节课上,我将不做任何实验,来向你展示为什么当你希望这个宇宙有普遍的属性时,你必须从这三个中选:(1)确定性,(2)经典概率论,(3)量子力学。
小于0%的机率
什么是拥有负数概念的“概率论”? 我们从来没有听说过天气预报说明天有-20%的可能性下雨,这是有悖常理的。先不管这些,让我们抽象地想想一个事件,拥有N个可能的结果。我们可以将这个事件用一个向量来表示。这个向量由N个实数构成:
(P1,...., Pn)
数学上我们会如何描述这个向量? 我们会说,这些概率应该是非负的,而且它们加起来等于1。后一条我们可以这样表示:概率向量的 1-norm 必须是1。(1-norm 指的是每个元的绝对值加和。)
但是 1-norm 并不是这个世界上唯一的 norm ,它并不是定义向量“大小”的唯一方式。还有另外的方式来定义,比如说 2-norm, 又叫 Euclidean norm (欧几里德范数)。欧几里德范数指的是向量元平方和的开平方值。
如何概率论是基于 2-norm 而不是 1-norm,那么量子力学就是其结果。
让我们来考虑一个比特。在概率论里,我们描述一个比特是 0 的可能性是 p,那么是 1 的可能性就是 1-p 。如果我们把 1-norm 变为 2-norm, 那么就不需要要求这两个数字加起来是1,而是要求它们的平方和是1。(假设这里讨论的数字还是实数。)换句话说,我们需要的是这样一个向量 (α,β), 满足 α^2 + β^2 = 1 (有谁知道markdown如何插入公式?)。 这样的向量组会形成一个圆:
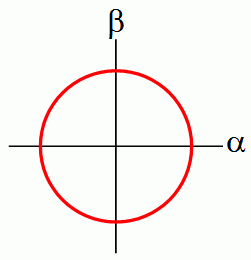
我们的理论必须的和观察有关, 假设有一个比特可以用这个向量(α,β)来描述,那么我们得说明当我们去看这个比特的时候会发生什么。既然它是一个比特,我们应该看到0或者1!而且看到0的几率和看到1的几率加起来应该是1。那么对于这个(α,β)向量,我们该如何得到两个加起来等于1的数字?很简单,我们可以让 α^2 作为结果是0的概率,让 β^2 作为结果是1的概率。
那么在这个情况下,我们可以不抛弃 α 和 β,直接用概率来描述这个比特?啊....关键的差别在于当我们把一个算子作用在向量上面时向量的变化(这个过程称为operation)。在概率论里,如果一个比特用向量(p,1-p)来表示,那么我们可以用一个随机矩阵(stochastic matrix)来表示任何对于向量的操作(operation)。
随机矩阵:一个矩阵由非负实数构成,每一列加起来和为1。
比如说,一个 “翻转比特”操作,把结果为1的概率从p变成了1-p,那么这个操作可以表示为:
(此处应有图)
未完待续 欢迎关注这篇文章,我会随时更新的。
2014年12月14日:
这文章烂尾了,未来某日也许会更新。