Given an array with n objects colored red, white or blue, sort them so that objects of the same color are adjacent, with the colors in the order red, white and blue.
Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.
Note:
You are not suppose to use the library's sort function for this problem.
大体意思是有一个颜色数组,包含红、白、蓝三种类型的颜色乱序排列在一起,让我们重新排列数组元素,使得同颜色的元素相邻。这个问题也叫荷兰国旗问题,因为我们可以将红、白、蓝三色想象成条状物,有序排列后正好组成荷兰国旗。
解法一:
- 遍历数组,统计红、白、蓝(0,1,2)三种元素的个数
- 根据三种颜色元素的个数重排数组
这种算法利用了计数排序的思想,时间复杂度O(n),代码如下
public class Solution {
public void sortColors(int[] nums) {
int red = 0;
int white = 0;
int blue = 0;
for (int i = 0; i < nums.length; i++) {
switch (nums[i]) {
case 0:
red++;
break;
case 1:
white++;
break;
case 2:
blue++;
break;
default:
break;
}
}
for (int i = 0; i < nums.length; i++) {
if (i < red) {
nums[i] = 0;
} else if (i < red + white) {
nums[i] = 1;
} else {
nums[i] = 2;
}
}
}
}
解法二:
利用快速排序partition过程的思想,我们可以把数组分成三部分,前部(全部是0),中部(全部是1)和后部(全部是2),每一个元素必属于其中之一。当我们把前部和后部各排在数组的前边和后边,中部自然就排好了。
设置两个指针begin和end,begin指向前部末尾的下一个元素(刚开始默认前部无0,所以begin指向第一个位置),end指向后部开头的前一个位置(刚开始默认后部无2,所以end指向最后一个位置),然后设置一个遍历指针current,从头开始进行遍历。
若遍历到的位置为1,则说明它一定属于中部,中部的我们都不动,然后current继续向后移动一个位置。
若遍历到的位置为0,则说明它一定属于前部,于是就和begin位置进行交换,然后begin向后移动一个位置。由于从begin位置交换过来的元素一定是已经遍历过的元素,所以current也向后移动一个位置。
若遍历到的位置为2,则说明它一定属于后部,于是就和end位置进行交换,然后end向前移动一个位置。由于从end位置交换过来的元素我们并没有遍历过,它可能是属于前部的,所以此时current并不向后移动。
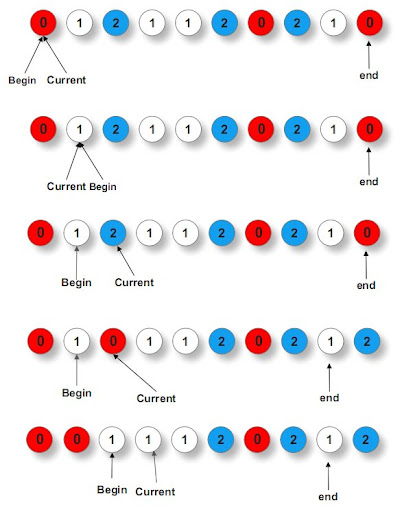

上述过程的代码如下,时间复杂度也为O(n)
public class Solution {
public void sortColors(int[] nums) {
int begin = 0;
int end = nums.length - 1;
int cur = 0;
while (cur <= end) {
if (nums[cur] < 1) {
swapElement(nums, begin, cur);
begin++;
cur++; // 从begin位置交换过来的元素一定是已经遍历过的元素
} else if (nums[cur] > 1) {
swapElement(nums, end, cur);
end--;
// 从end位置交换过来的元素我们并没有遍历过
} else {
cur++;
}
}
}
public void swapElement(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
对于快速排序,虽然它不能保证在最坏情况下仍为O(nlogn)的时间复杂度(主要原因在于基准的不确定性,有可能遭遇每次选取的基准都是最值的情况),但它的partition过程仍有着广泛的应用价值。
著名的BFPRT算法就是先通过巧妙的方式(中位数的中位数)选取基准,再利用快速排序的partition过程,实现了在最坏情况下仍然可以在线性时间复杂度内从任意的无序数组中找到第K小(大)的元素,即解决top K问题。