贝叶斯分类器

朴素贝叶斯，

简单代码可参考： https://github.com/AresAnt/ML-DL

贝叶斯其实是一个比较简单的多分类问题，简单来说，就是通过输入的样本对于分类的概率。
P(A|B) = P(B|A) P(A) / P(B) 【一般表示为 B为样本集合，A为分类集合】

P(A) 也称为先验概率，举个例子，比如说一个二分类器，它的集合 Y = { y1 , y1 , y2}
那么 P(A) 的先验概率为：

P(A_y1) = 2 / 3
P(A_y2) = 1 / 3

P(B|A) 被称为类条件概率，也是“似然”概率，表现为，在A的条件集合下，B发生的概率。举个例子，假设同样是一个二分类问题。它的集合 X = { (x1,y1) , (x1,y2) , (x2,y1) , (x1,y1) }
那么P(B|A)的似然概率可以写为：

P(x1|y1) = 2 / 3 【我们可以看到集合X中总共有3个y1数据，而三个y1数据中含有两个x1数据】
p(x1|y2) = 0 / 1 【这里为0其实有另外的处理，拉普拉斯修正，后面会讲解】
p(x2|y1) = 1 / 3
p(x2|y2) = 0 / 1

朴素贝叶斯

假设某个体有n项特征（Feature），分别为F1、F2、...、Fn。现有m个类别（Category），分别为C1、C2、...、Cm。贝叶斯分类器就是计算出概率最大的那个分类，也就是求下面这个算式的最大值：

P(C|F1F2...Fn) = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

由于 P(F1F2...Fn) 对于所有的类别都是相同的，可以省略，问题就变成了求:

P(F1F2...Fn|C)P(C)

朴素贝叶斯分类器则是更进一步，假设所有特征都彼此独立，因此

P(F1F2...Fn|C)P(C) = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

到这里就变成我们上面的上述例子了。但是我们会发现，如果这样累乘的过程中，只要出现了0这一项，那么这项数据就会变的没有意义。所以这里会延伸出“拉普拉斯修正”。

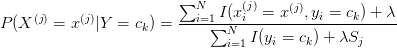
当λ=0，就是最大似然估计，λ=1就是拉普拉斯平滑。

拉普拉斯平滑：就是在分子中加1，分母中加上该样本的类别数【比如说，人种可分为白人，黑人，黄种人，即 x1 = { 白人，黑人，黄种人 } 中的一个，那么这个类别数就是3】，以这样的方式来避免出现0数的可能性。

极大似然估计：
极大似然法，我们知道在数据中会存在离散型数据与连续性数据，一般对于连续性数据，我们会在做Bayes时候会找原先训练集中找不到相同数据。但是，我们仍然需要对这类测试数据给予一个值，这里我们就用到了极大似然估计法，通过将原有的数据通过一个函数，映射成一定概率分布的模型（一般正太分布遇到的比较多）【补充：离散型数据也会有概率分布模型，一般来说离散型数据的似然函数基本为指示函数，所以一般离散型数据会不做处理】。通过映射成的概率分布模型，我们就可以对传入的测试数据进行概率赋予。

注：
--- 极大似然估计：意思就是用训练集样本去估计出集合Y中某样本y_i能够出现的概率，因为集合Y中y_i具有多个，最大值的y_i即为我们想要找寻的“可能性”最大的值，即为极大似然估计。
--- 极大似然法：是在极大似然估计中 y_i 对 X 集合中的某样本 x_i（feature）求最大可能值的做法。

算法流程不做赘述：可以参考该网页的例子进行操作，比较简单，就是概率的计算累加比较等。
http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html
【周志华的西瓜书p150页的例子也极为浅显易懂，可以参考，鄙人代码则是按照其书进行编写】

最后编辑于：2017.12.02 21:01:27