调用
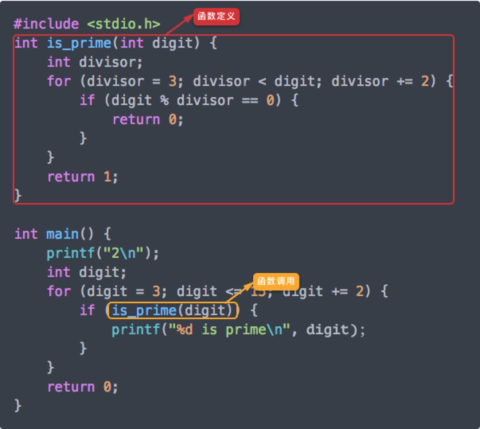
首先要理解的是函数的 定义(define) 和 调用(call)。
被抽出的函数is_prime的整体被称为函数定义。
下面黄色标记的地方,是函数的使用过程,称为函数调用。
形参和实参
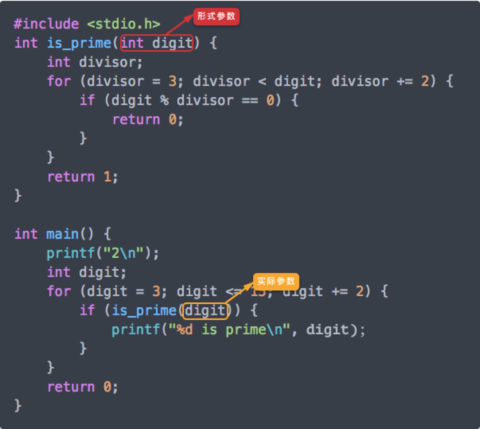
在定义一个函数时,如图中的红框所示,我们需要将这个函数可以接收的参数都列在函数名后的小括号内,并且列出每一个参数的类型。我们称在函数定义中列出的这些参数为 形式参数(formal parameter)。
相对应的,我们在调用函数时,如黄框所示,需要传入一个值,期待被所调用的函数所接收和使用。我们称在调用函数时所传入的参数为 实际参数(actual parameter)。一个函数也并不一定只有一个参数,一个多参数的函数在定义函数时,小括号内要列出每一个参数,参数之间需要用逗号分隔。
不同作用域内,哪怕变量名相同,也需要分别在对应的作用域内声明变量和使用。
递归调用
我们称这种在一个函数的定义中调用自身的情况为 递归调用(recursive call)。
头递归
下面这个函数就是一个递归实现的计算阶乘的函数。在一般条件(如这里的n == 1)满足时,返回一个确定的值,而在其他情况下,返回一个包含本身函数的递归调用的这种递归设计,被我们称为 头递归(head recursion)。
int factorial( int n)
if (n==1){
return 1;
}
return factorial(n-1)*n;
尾递归
int factorial( int n, int product)
if (n==0){
return product;
}
product = product * n;
return factorial(n-1) * product;
可以对比一下头递归和尾递归实现的函数从被调用到返回的过程。

头递归在进行下一层的调用前,没进行计算。在下一层返回后,才完成了这一层的计算。

尾递归在进行下一层的调用前,会先进行计算,而在最终一般条件满足时,会将计算的结果逐层直接返回。
声明与实现的分离
在实际的工作中,可能会碰见主函数中“调用函数的定义的位置在主函数之后”这样的情况,实际上这时候,因现在的代码框中可以看到我们在之前的课程中定义出的f和h函数。如果把我们把f函数和h函数的定义放到main函数的后面,会发生编译错误呢?
因为我们在main函数中调用了f函数和h函数,但在调用之前并没有定义这两个函数,所以编译器就愉快地罢工啦。所以呢,如果我们采用直接定义的方式来创造函数的话,我们就需要时时刻刻关注这些函数之间的依赖关系,并且把他们正确地排序。
然而,随着程序规模的增长,总要关注函数的依赖关系并且对函数进行排序,会给我们带来不小的工作量。所以 C 语言中给我们提供了一个从这个问题中解脱的方式——函数的声明与实现分离。如下
#include <stdio.h>
#include <math.h>
double f(double a ,double b);
double h(int x);
int main() {
double x;
double y;
double z;
x = f(1, 0.5);
y = f(2, 0.25);
z = h(x);
printf("%g\n%g\n%g\n", x, y, z);
return 0;
}
double f(double a, double b) {
return sqrt((a - cos(b)) / 2);
}
double h(int x) {
return 2 * x + f(3, 0.15);
}
实际上在这段代码中
double f(double a ,double b);
double h(int x);
就是先声明了。实际上声明的时候甚至里面的变量名都不用写,直接写类型就行了,也是可以正常通过的。
double f(double ,double );
double h(int);
命名的学问
- 如果程序中有一个变量叫做 a,表示苹果,就不如直接使用 apple 作变量名。
- response, resource, resolve, resolution 就都算是可以被接受的命名,而 res 这样一个很难让人知道指代的缩写则不应该被用于命名。
- 用 i_can_read 这样的形式命名,而不是 iCanRead 这种形式的命名。
- 命名是个有学问的事情,不同团队会有不同规范。
函数的变量
变量的值、变量的地址可以做函数的参数,函数也可以作为函数的参数。
如果一个函数可以被传入另一个函数,当传入的函数不同时,同样的一个被传入函数就可能会产生不同的功能。
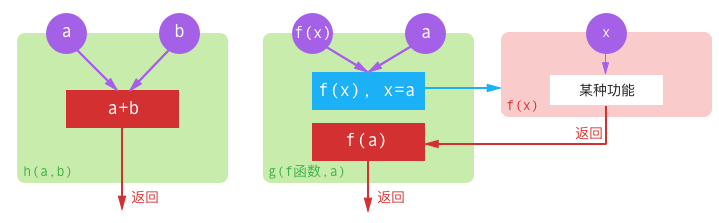
C 语言中函数和变量类似,也是有自己的内存地址的。但是,函数不像变量一样可以进行值传递,我们在将其作为函数参数进行传递时,需要传递它的地址。
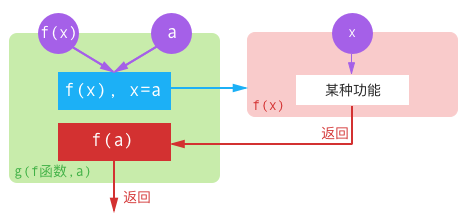
对于上面这种用情况,函数g需要有一个形式参数用于接收函数地址。我们将得到一个如下面所示形式的函数。在这个函数定义中,第一个参数需要一个返回值类型为float且有一个int类型参数的函数,第二个参数就是普通的int类型的值。
int g(float(*f)(int), int a){
return f(a);
}
对这样一个函数g,使用其函数名时,其实是在使用它的地址。因此,我们在接到形式参数中的函数地址后,我们可以直接写 f(a)。这与我们用取值符取出函数地址并进行函数调用 (*f)(a) 的方式是等价的。
不同于传变量地址时需要用取值符的做法,在调用上面这个g函数,并且将函数地址作为参数时,直接将函数名传入就可以了。如果我们希望将
float sqrt_minus_one(int a){
return sqrt(a)-1;
}
作为参数,和变量number一起传入给g,那么,调用时则应该写:
g (sqrt_minus_one, number);
将sqrt_minus_one函数和变量a传入到了g后,形式参数float (*f)(int)接收了sqrt_minus_one函数的地址,形式参数int a接收了number的值。
int g(float(*f)(int), int a){
return f(a);
}
接下来,通过f(a)的方式,传入的函数sqrt_minus_one被调用,并将a作为参数传入到了sqrt_minus_one函数中。
sqrt_minus_one函数接收到了值后进行了计算并返回,在g函数中,计算结果返回。至此,最初调用的位置得到了计算的最终结果。
我们可以看到,函数地址做函数参数的方式可以大大地增加函数的灵活性。我们将在后面的学习中自己试一试这样的使用方式喔。
#include <stdio.h>
#include <math.h>
#define EPSILON 1e-6
double f(double x) {
return 2 * pow(x, 3) - 4 * pow(x, 2) + 3 * x - 6;
}
double f_prime(double x) {
return 6 * pow(x, 2) - 8 * x + 3;
}
double h(double x) {
return pow(x, 3) - 4 * pow(x, 2) + 3 * x - 6;
}
double h_prime(double x) {
return 3 * pow(x, 2) - 8 * x + 3;
}
double newton(double (*f)(double),double (*f_prime)(double)) {
double x = 1.5;
while (fabs(f(x)) > EPSILON){
x = x - f(x) / f_prime(x);
}
return x;
}
int main() {
printf("%g\n", newton(f, f_prime));
printf("%g\n", newton(h, h_prime));
return 0;
}