今天我们来讲解一下上一篇的课后习题。
1. 题目
编程实现把1~9九个数字填入九宫格中,满足每行、每列和对角线上的三个数字和为15。如图所示。
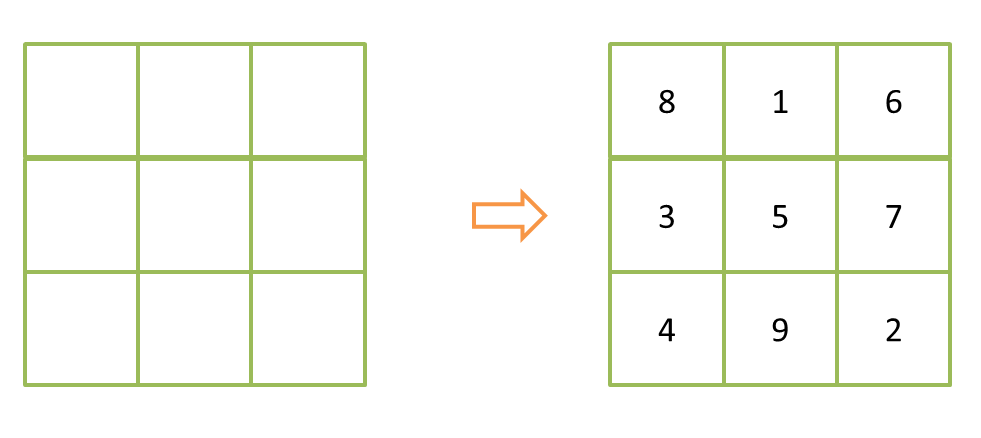
注意:由于结果不唯一,只要打印出一种满足条件的结果即可。
2. 分析
这道题目很多同学拿到后觉得无从着手,完全和学过的知识没有一点联系。其实,这道题用到的就是学过的知识。
2.1 建模
首先,这道题是一个3 * 3的二维数组,要把9个数填进去。在众多的可能性中找到一个满足条件的即可。
接下来,我们想想之前讲到的二维数组和一维数组的关系,是不是可以把这道题转化成一个9个元素的一维数组,把9个数字排列组合放进这个数组中。这就和之前抛硬币的那道题有几分相像了。

如图所示,可能出现的情况应该共有9!种。我们要做的就是编程穷举出所有的可能性,在这个过程中判断每种可能性是否满足题目要求。
注意:这个解法并不是最优解,但却是最适合初学者学习的。我在如何评价一段代码中已经阐明了我的观点。
2.2 功能分解
有了一个基本的模型,我们可以把问题转化为几个子功能:
- 计算排列组合
列举出所有的可能,拿到9!个二维数组。
- 判断
判断得到的每个结果是否符合要求。
3. 判断功能
判断的条件比较简单,就是要每行数字、每列数字和两个对角线的数字之和均为15。大部分人很容易想到这种写法:
#define MAX_SIZE 3
int g_arr[MAX_SIZE][MAX_SIZE];
int Calculate()
{
int i, j, sum;
// 计算3行
for (i = 0; i < MAX_SIZE; i++)
{
sum = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sum += g_arr[i][j];
}
if (sum != 15)
{
return 0;
}
}
// 计算3列
for (i = 0; i < MAX_SIZE; i++)
{
sum = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sum += g_arr[j][i];
}
if (sum != 15)
{
return 0;
}
}
// 计算对角线
sum = 0;
for (i = 0; i < MAX_SIZE; i++)
{
sum += g_arr[i][i];
}
if (sum != 15)
{
return 0;
}
sum = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sum += g_arr[i][MAX_SIZE- 1 - j];
}
if (sum != 15)
{
return 0;
}
return 1;
}
Calculate()函数的功能是判断二维数组g_arr是否满足要求,如果满足返回1,如果不满足返回0。
这个函数功能上没有问题,但使用了太多次循环,执行效率太低。不过细心的同学肯定已经发现有些统计其实可以合并在一起做。我对这段代码做了优化,修改如下:
int Calculate()
{
int i, j;
int sumLine, sumCol, sumDL1, sumDL2;
sumDL1 = 0;
sumDL2 = 0;
for (i = 0; i < MAX_SIZE; i++)
{
sumLine = 0;
sumCol = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sumLine += g_arr[i][j];
sumCol += g_arr[j][i];
}
if (sumLine != 15 || sumCol != 15)
{
return 0;
}
sumDL1 += g_arr[i][i];
sumDL2 += g_arr[i][MAX_SIZE- 1 - i];
}
if (sumDL1 != 15 || sumDL2 != 15)
{
return 0;
}
return 1;
}
这段代码只用了一组嵌套的for循环,通过四个变量统计出了所有数据。变量sumLine和sumCol分别用来计算每一行和每一列的数字之和。这里只是在循环中修改了一下i和j的下标顺序就完成了两个维度的统计。变量sumDL1和sumDL2分别计算了两条对角线上数字之和。
sumDL1 += g_arr[i][i];
sumDL2 += g_arr[i][MAX_SIZE- 1 - i];
这两行代码用了在天花板编程手把手计划-第1期-第2天中介绍的方法,忘记的同学可以回去复习。
4. 打印
这里依然需要一个二维数组打印的函数,这和前面几个题目相似,不用多说了。
void PrintMap()
{
int i, j;
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
printf("%3d ", g_arr[i][j]);
}
printf("\n");
}
printf("\n");
}
5. 计算排列组合
这里依然需要用到一个递归的方法。每一次递归都给一个对应的位置填写一个数字。这里和抛硬币问题有一个唯一的不同,就是每个数字只能填一次。
5.1 排除法
Aha_斌同学是第一个完成这道题目的,他用的办法是这样。
首先,用抛硬币的方法找出允许重复情况下的可能矩阵。之后逐一判断,如果发现有重复数字就舍弃那种情况。
这个解法很聪明,一下就解决了问题,而且不需要太复杂的算法。代码大家可以去参考他发的作业帖。
5.2 用数字作递归条件
我要介绍的算法是另外一个思路,不是按照每个空格去递归,而是按照数字去递归。通过递归的方式执行九次动作,每次负责把一个数填在一个空格中。这样永远不会出现重复数字的问题。
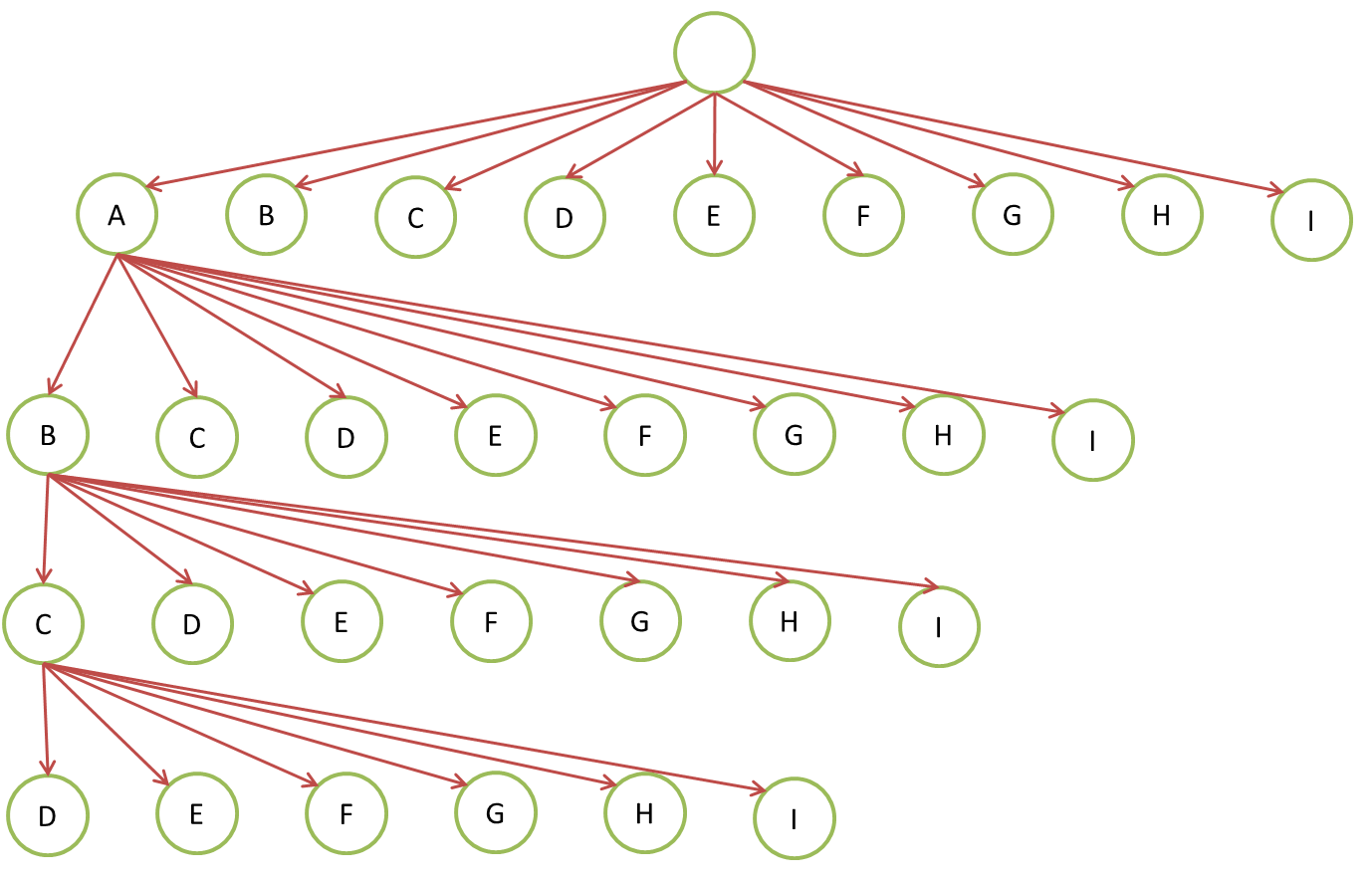
图中用A~I表示9个空格,整个递归的过程是一棵不规则的N叉树。根结点有9个子节点,第一层的每个节点有8个子节点,第二层的每个节点有7个子节点,以此类推。图中只画出了一个分支的前三次迭代。
现在剩下最后一个问题,每次递归时如何为不同的层执行不同次数的递归呢?
方法一:状态恢复法
另外创建一个二维数组纪录下当前被使用的格子和未使用的格子。每层递归函数返回时把填写过的格子更新成未使用的格子。
这个方法很容易想,但要多维护一个二维数组,而且有太多批量赋值的工作,不适合初学者。
方法二:利用数字特性
我使用了一种更巧妙的方法,我先把九个格子都初始化为0,再让递归按照从大到小的顺序填写数字,当空格中存在比当前数字小的数字时,说明这个格子没有在这个分支中被使用过。
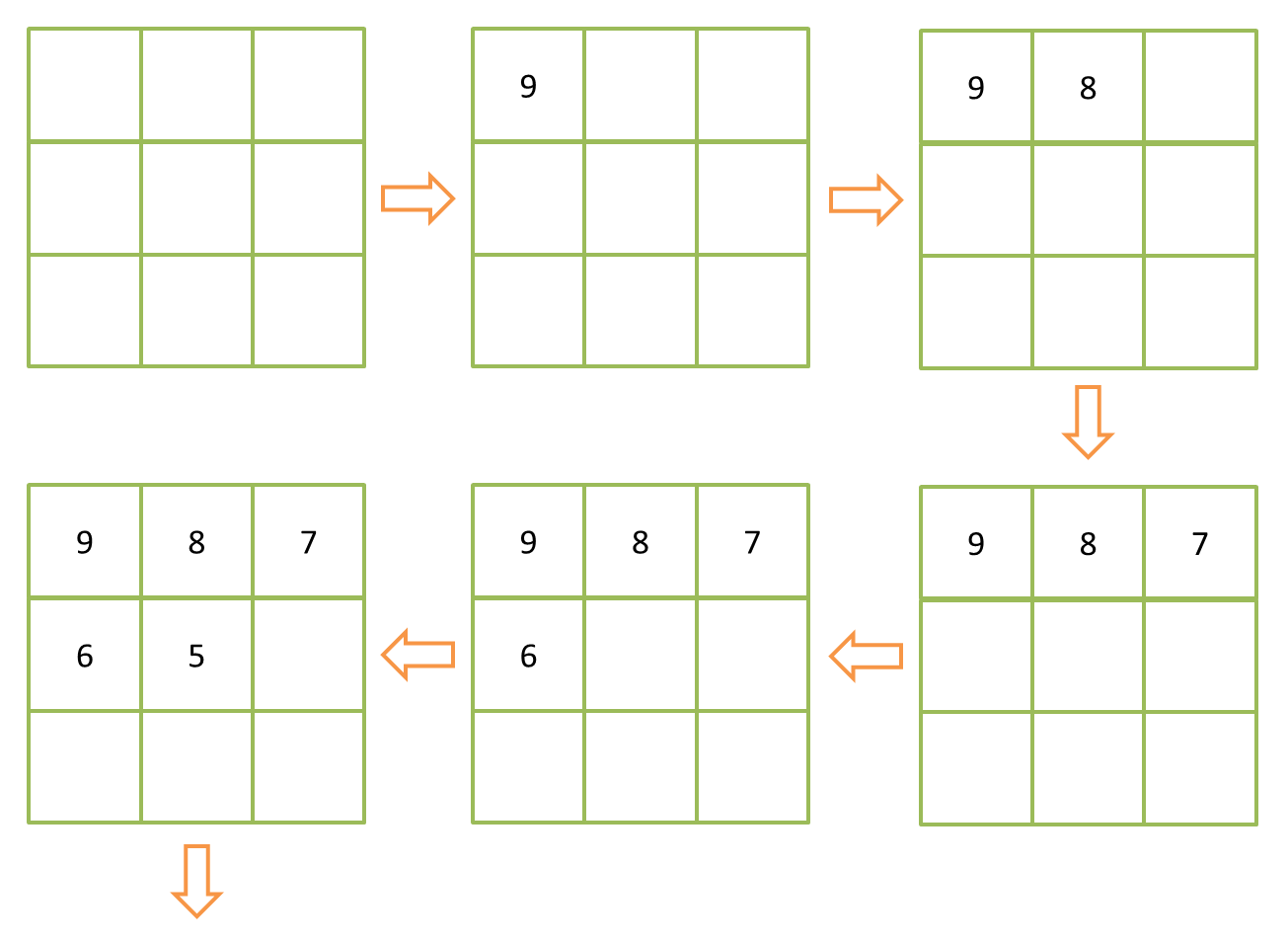
代码如下:
int g_cnt = 0;
void FillBlank(int num)
{
int i;
int nBak;
int* pArr = (int*)g_arr;
if (num <= 0)
{
if (Calculate() == 1)
{
PrintMap();
}
printf("%d\r", g_cnt++);
return;
}
for (i = 0; i < MAX_SIZE * MAX_SIZE; i++)
{
if (num >= pArr[i])
{
nBak = pArr[i];
pArr[i] = num;
FillBlank(num - 1);
pArr[i] = nBak;
}
}
}
函数FillBlank()的功能是把数字num填在一个空格中。每一层递归函数调用下一层函数时,传递一个num - 1。当参数为0时,说明这个分支到达最低端的叶子节点。这时候二位数组中保存的是一个完成的可能。通过Caculate()函数判断它是否符合题意,如果符合就打印出来。这里打印的是所有符合题意的可能。
在FillBlank()中,我们通过一个循环遍历九个空格,当要填写的数字大于格子中的数字时,说明可以填写。这样就保证了每一层的填写次数正确。
最后,在填写数字之前,需要先用nBak变量保存空格中原有的数字,在这一轮递归结束后要恢复回来。原因大家好好思考一下。
注意:由于穷举的次数太多,等待的过程会比较漫长,我们在这里加入了一个显示当前寻找次数的功能。全局变量g_cnt记录了找到的可能性次数,通过printf("%d\r", g_cnt++);不断打印在屏幕上。
6. 功能调用
main()函数变得非常简单:
int main()
{
FillBlank(9);
return 0;
}
我们执行一下,效果如下:

7. 留下一种结果
对现有的程序稍作修改,我们只需要一个符合题意的结果即可。代码如下:
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#define MAX_SIZE 3
int g_arr[MAX_SIZE][MAX_SIZE] = { 0 };
int Calculate()
{
int i, j;
int sumLine, sumCol, sumDL1, sumDL2;
sumDL1 = 0;
sumDL2 = 0;
for (i = 0; i < MAX_SIZE; i++)
{
sumLine = 0;
sumCol = 0;
for (j = 0; j < MAX_SIZE; j++)
{
sumLine += g_arr[i][j];
sumCol += g_arr[j][i];
}
if (sumLine != 15 || sumCol != 15)
{
return 0;
}
sumDL1 += g_arr[i][i];
sumDL2 += g_arr[i][MAX_SIZE - 1 - i];
}
if (sumDL1 != 15 || sumDL2 != 15)
{
return 0;
}
return 1;
}
void PrintMap()
{
int i, j;
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
printf("%3d ", g_arr[i][j]);
}
printf("\n");
}
printf("\n");
}
int g_cnt = 0;
int g_return = 0;
void FillBlank(int num)
{
int i;
int nBak;
int* pArr = (int*)g_arr;
if (g_return == 1)
{
return;
}
if (num <= 0)
{
if (Calculate() == 1)
{
PrintMap();
g_return = 1;
}
printf("%d\r", g_cnt++);
return;
}
for (i = 0; i < MAX_SIZE * MAX_SIZE; i++)
{
if (num >= pArr[i])
{
nBak = pArr[i];
pArr[i] = num;
FillBlank(num - 1);
pArr[i] = nBak;
}
}
}
int main()
{
FillBlank(9);
return 0;
}
执行效果如下:

由于这个递归方法比较抽象,不理解的同学可以在群里提问,我再仔细讲解一下。
8. 课后练习
给出一组代数表达式,请编程判断出他们的括号是否配对正确。
8.1 输入内容
5
[a+(b+c)]*(a+b]
(a-1+b)-(b+c)
x-[a*(b+c))]
a+(b+c+(d-(e+m))
a+b+[c-d*e-(a-b)-c]
第一行中的5表示共有5个表达式需要判断。下面的每一行有一个表达式。要求把这组数据原样保存在文件input.txt中,通过读文件的方式读入数据完成判断。
8.2 输出
括号匹配正确打印1,匹配错误打印0。正确的输出结果应该是:
0
1
0
0
1
我是天花板,让我们一起在软件开发中自我迭代。
如有任何问题,欢迎与我联系。