简单选择排序(SelectSort)
选择排序思想很简单,对所有元素进行遍历,选出最小(或最大)的元素与第一个元素进行交换,然后逐次缩小遍历的范围。
public void sort(int[] items) {
for (int i = 0; i < items.length; i++) {
int minIndex = i; //最小元素的index
for (int j = i; j < items.length; j++) {
if (items[j]<items[minIndex])) {
minIndex = j;
}
}
int temp = items[i]; //从左开始放最小的
items[i] = items[minIndex];
items[minIndex] = temp;
}
}
冒泡排序:
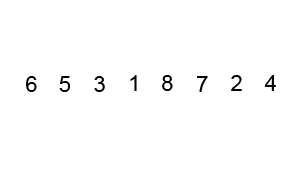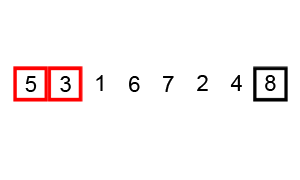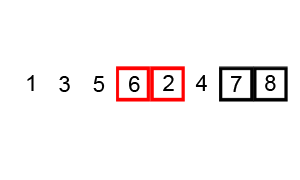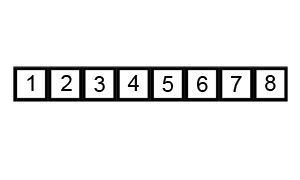
最右边的先排好
public static void maopao(int[] array){
for (int i = 0,n=array.length; i < n; i++) {
for (int j = 0; j < n - 1 - i; j++) {
swapIf(array,j,j+1);
}
}
}
选择排序:
插入排序:

扑克牌
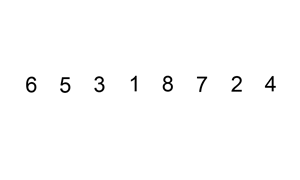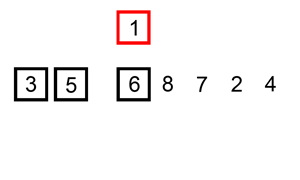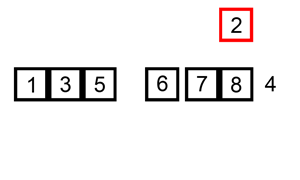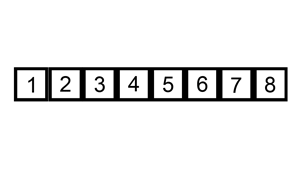
归并排序:

image.png
伪代码:
//伪代码
public void mergeSort(int[] nums, int L, int R) {
if (L == R) { //如果只有一个元素,那就不用排序了
return;
} else {
int M = (R + L) / 2; //每次取中间值
mergeSort(nums, L, M); //通过递归再把左边的按照这个方式继续不停的左右拆分
mergeSort(nums, M + 1, R); //通过递归再把右边的按照这个方式继续不停的左右拆分
merge(nums, L, M + 1, R); //合并拆分的部分
}
}
堆排序
二叉堆
二叉堆是完全二叉树, 保证头结点是最大/最小的。
二叉堆主要的应用击中在两个地方一个是排序,一个是基于优先级队列的算法。
插入一个元素时我们通常要做的就是有三步:
- 把要插入的节点放在二叉堆的最末端
- 把这个元素和它的父节点进行比较,如果符合条件或者该节点已是头结点插入操作就算完成了
- 如果不符合条件的话就交换该节点和父节点位置。并跳到第二步。
- 插入节点不停向上比较的过程叫做向上整形。
插入

我们插入15,位置为X

X的父节点是8,X与8进行比较,发现X(15)大于8于是8与15互换。

X(15)接着和11比较,发现15比11大于是互换。
删除
二叉堆的删除操作指的是删除头结点的操作,也就是最小或者最大的元素。删除操作分为三步:
- 首先将头结点与最后一个节点位置互换(互换之后的最后一个节点就不再视为二叉堆的一部分)。(最后一个节点是完全二叉树最右下角的?)
- 将互换之后的新的头结点与子节点进行比较,如果符合条件或者该节点没有子节点了则操作完成。
- 将它和子节点互换,并重复步骤2。(如果它的两个子节点都比它大/小,那么它与其中较大/小的一个互换位置。)
image.png
删除头结点11,我们将11头结点与最末一个节点4互换。
将4与它的子节点中较大的一个进行互换、然后继续进行步骤2,但是、节点4已经没有子节点于是操作结束。
堆排序
堆排序其实分为以下几步:
1:首先将待排序的n个元素构建一个二叉堆array[n]
2:执行删除操作,只是这里我们并不是删除头结点,而是将头结点换到二叉堆末尾,并形成一个出去队列末尾的新二叉堆。
3:重复步骤2,直到删除了最后一个元素。
这个过程其实就是先构建一个最大/最小二叉堆,然后不停的取出最大/最小元素(头结点),插入到新的队列中,以此达到排序的目的。
广度优先搜索BFS:
解决两类问题:
- 节点A又前往节点B的路径吗:芒果销售商问题
- 从节点A前往节点B哪条路最短:最短路径问题
采用队列来缓存,先将第一级朋友加进去,挨个检查,假如该朋友不是芒果销售商,则把他所有的朋友(二级朋友)插入队列尾部。还需要一个列表存放检查过的朋友,因为关系可能有环。-这样其实也解决了最短路径问题。
狄克斯特拉算法
解决加权图,开销最小的(限制挺多的)
- 只适用于有向无环图
- 对于处理过的节点,没有前往该节点的更短路径,也就是不能再次处理一个节点。或者说不能有负权
- 图中包含负权边的,使用贝尔曼-福德算法
1.每个节点有父节点和开销
2.先找自己能到的最近的节点,更新其父节点及开销,其他达不到的节点开销设为无穷大
3.按开销最小顺序遍历最近节点,更新其他节点的父节点和开销
4.一直按开销从小到大顺序遍历,遍历过的不在遍历
换钢琴
贪婪算法:
贪婪算法易于实现,运行速度快,是不错的近似算法。
每一步都采取最优的做法。基本能拿到一个近似最优解的
动态规划:
先解决子问题,在解决大问题。
动态规划先决条件:每个子问题都是离散的,即不依赖其他子问题。
背包问题:

背包拆格
最终解:

背包最终解
课后题:

image.png
最长公共子串:

image.png
最长公共子序列:

image.png
K最近邻算法
多维空间最短距离:毕达哥拉斯
实际常采用:余弦相识度(多维空间夹角余弦)

image.png
快速排序快排比较
-
两端扫描交换方式
image.png
public static void QuickSort(int[] nums, int start, int end) {
//如果start >= end了,说明数组就一个数了。不需要排序
if(start >= end){
return;
}
//取第一个数为参考值
int data = nums[start];
int i = start, j = end;
//当 i 和 j 还没有碰到一起时候,一直重复移动 j 和 i 等操作
while (i != j) {
//当 j 位置比参考值大的时候,继续往左边移动,直到找到一个比参考值小的数才停下
while (nums[j] >= data && i < j) {
j--;
}
//当 i 位置比参考值小的时候,继续往右边移动,直到找到一个比参考值大的数才停下
while (nums[i] <= data && i < j) {
i++;
}
//交换二边的数
if (i < j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
}
//当退出上面的循环,说明 i 和 j 的位置交汇了,更换参考值与 i 位置的值。
nums[start] = nums[i];
nums[i] = data;
//左边的数组通过递归继续调用,这时候因为参考值在 i 的位置,所以左边是从start 到 i -1
QuickSort(nums, start, i - 1);
//右边的数组通过递归继续调用,这时候因为参考值在 i 的位置,所以右边是从 i -1 到 end
QuickSort(nums, i + 1, end);
}
2.填坑方式:

填坑方式
public void fillSort(int[] items, int start, int end) {
if (start < end) {
int pivot = items[start];
int i = start, j = end;
while (i < j) {
while (i < j && items[j] > pivot)
j--;
items[i] = items[j];
while (i < j && items[i] <= pivot)
i++;
items[j] = items[i];
}
// 相遇后i == j,此处是个坑
items[i] = pivot;
fillSort(items, start, i - 1);
fillSort(items, i + 1, end);
}
}




