初中学了简单了胡克定律,高中的时候力变成了向量,而大学里应力应变都变成了2阶张量,同样是胡克定律,在不同的尺度下,却有不同的含义。
标量尺度
我们初中学过胡克定律,即在弹性范围内,弹簧的伸长和所施加的力成正比:

用公式表达就是:

这里k是一个实数,表明了弹簧的性质,当弹簧压缩时,该式任然成立,只是F和X前面变成了负号。
向量尺度
高中时,力F变成了向量,位移X也变成了向量,什么是向量?既有大小又有方向的量就是向量,和标量尺度的胡克定律比较,引进向量其实就是引进了方向,但是各个方向上任然满足标量形式的胡克定律,胡克定律的公式没变,只是其中的F和X是向量了,这时如果将胡克定律在直角坐标系下展开:

即:
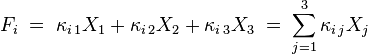
其中i从1到3.
所以,胡克定律:

任然成立,只是这里的F和X是向量,而kappa不再是一个实数(标量),而是一个2阶张量。
张量尺度
在大学里学了连续介质力学,这时的胡克定律变成了:
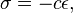
其中sigma是应力张量(2阶),epsilon是应变张量(2阶),而c是一个刚度张量(4阶)
在直角坐标系下,应力张量和应变张量可以表示为矩阵的形式:
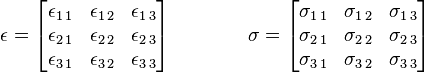
而4阶的刚度张量在直角坐标系下:

一共有3*3*3*3=81个元素。
所以直角坐标系下的胡克定律可以写为:

刚度张量的简化
有以上可知,刚度张量有3*3*3*3=81个元素,那能不能将他简化呢?
小的对称minor symmetries
由于柯西应力张量的对称性:

我们可以得到:

同样的,由于应变张量的对称性,我们可以得到:

这样刚度张量的元素个数就从81个减小到了36个。
在直角坐标系下,这时的应力应变张量可以表示为:

而刚度张量的36个元素可以表示为:

注意:由于对称性,这时的刚度张量已从4阶变成了2阶。
大的对称major symmetries
由于应力应变张量同时变化,应力应变关系可以从应变能量密度(U)的微分得到:

由于积分顺序的任意性,我们可以得到:

这样刚度张量的元素个数就从36个减小到了21个。
在直角坐标系下,这时的刚度张量的矩阵表示:

是一个对称矩阵,所以只有6+5+4+3+2+1=21个元素。
其他对称性
以上的两种对称一般的材料都会有,而接下来的这些对称性确是只有在特定条件下才能满足:

正交对称Orthotropic
正交对称有两个对称面(可以证明:有两个对称面一定会有第三个),典型的正交对称材料是木头

木头的性质沿着半径方向,圆周方向以及轴向是不同的。
在直角坐标系下,如果坐标基矢量e1,e2,e3垂直于3个对称面,那么刚度张量元素个数可以从21个减小到9个:

横断对称Transversely isotropic
横断对称有一个对称轴,很多复合材料和生物薄膜材料都是横断对称的。
在直角坐标系下,如果坐标基矢量e3和对称轴重合,那么刚度张量元素个数可以进一步从9个减小到5个:

立方对称cubic symmetry
立方对称是最简单的各向异性情况,这时刚度矩阵元素个数为3个:

各向同性isotropic
终于到了各向同性,这一我们最常应用的情况,各向同性的材料,顾名思义,材料在各个方向上的性质是一样的,也可以说它有无穷多个对称面。各向同性的材料,刚度矩阵元素个数为2。
在直角坐标系下,公式表示为:

矩阵表示为:

其中,lamda等于:
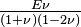
u等于:

所以上式变为:

总结
仿佛坐了一次过山车,从初中学过的最简单形式的胡克定律开始(此时弹性系数k为一实数),到向量形式的胡克定律(此时k为一2阶张量,含9个元素),最后到连续介质力学中张量形式的胡克定律(此时k为一4阶张量,含81个元素),然后由于对称性,元素个数不断减少,在各向同性材料里,k只有两个元素。从中可以看出,升阶其实就是将更多方向性考虑进去,这样就需要更多的元素表示不同的方向,而对称性又决定了我们可以用同一元素代表不同方向的性质。我们从“1”出发,最后回到了“2”。
参考文献
wikipedia_Hooke's law
Linear elasticity
Orthotropic material