前言:
以斯坦福cs231n课程的python编程任务为主线,展开对该课程主要内容的理解和部分数学推导。该课程相关笔记参考自知乎-CS231n官方笔记授权翻译总集篇发布课程材料和事例参考自-cs231n
本章为线性分类器的softmax讲解,紧接上章的SVM,其中涉及到的一些线性分类器的知识已经在上章说明,本次便不再赘述。cs231n课程作业assignment1(SVM)
SoftMax分类器简介:
Softmax和SVM同属于线性分类器,主要的区别在于Softmax的损失函数与SVM的损失函数的不同。Softmax分类器就可以理解为逻辑回归分类器面对多个分类的一般化归纳。SVM将输出f(x_i,W)作为每个分类的评分,而Softmax的输出的是评分所占的比重,这样显得更加直观。
在Softmax分类器中,函数映射f(x_i;W)=Wx_i保持不变,但将这些评分值视为每个分类的未归一化的对数概率,并且将折叶损失(hinge loss)替换为交叉熵损失(cross-entropy loss)。公式如下:
)
或
在上式中,使用f_j来表示分类评分向量中f的第j个元素个,数据集的损失值是数据集中所有样本数据的损失值的均值与正则化损失R(W)之和。其中Softmax函数为:
 = \frac{e{z_j}}{\sum_ke{f_j}})
其输入值是一个向量,向量中元素为任意实数的评分值(z中的),函数对其进行压缩,输出一个向量,其中每个元素值在0到1之间,且所有元素之和为1。
除了损失函数不同,其他的操作与SVM基本相同,进一步的讲,SVM分类器使用的是折叶损失(hinge loss),而Softmax使用的是交叉熵损失(corss-entropy loss),本质上都属于线性分类器的一种。
Softmax与SVM比较:
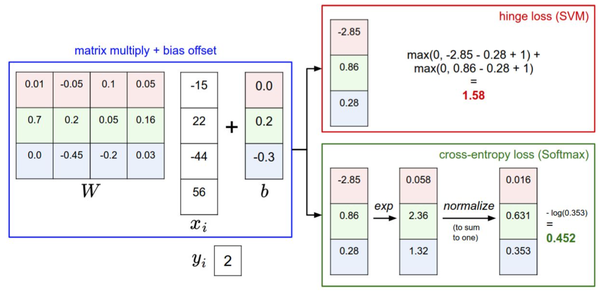
针对一个数据点,SVM和Softmax分类器的不同处理方式的例子。两个分类器都计算了同样的分值。不同之处在于对$f$分值的解释:SVM分类器将它们看做是分类评分,它的损失函数鼓励正确的分类(本例中是蓝色的类别2)的分值比其他分类的分值高出至少一个边界值。Softmax分类器将这些数值看做是每个分类没有归一化的对数概率,鼓励正确分类的归一化的对数概率变高,其余的变低。SVM的最终的损失值是1.58,Softmax的最终的损失值是0.452,但要注意这两个数值没有可比性。只在给定同样数据,在同样的分类器的损失值计算中,它们才有意义。
在实际使用中,SVM和Softmax经常是相似的:通常说来,两种分类器的表现差别很小,不同的人对于哪个分类器更好有不同的看法。相对于Softmax分类器,SVM更加“局部目标化(local objective)”,这既可以看做是一个特性,也可以看做是一个劣势。考虑一个评分是[10, -2, 3]的数据,其中第一个分类是正确的。那么一个SVM(&$Delta =1$)会看到正确分类相较于不正确分类,已经得到了比边界值还要高的分数,它就会认为损失值是0。SVM对于数字个体的细节是不关心的:如果分数是[10, -100, -100]或者[10, 9, 9],对于SVM来说没设么不同,只要满足超过边界值等于1,那么损失值就等于0。
对于softmax分类器,情况则不同。对于[10, 9, 9]来说,计算出的损失值就远远高于[10, -100, -100]的。换句话来说,softmax分类器对于分数是永远不会满意的:正确分类总能得到更高的可能性,错误分类总能得到更低的可能性,损失值总是能够更小。但是,SVM只要边界值被满足了就满意了,不会超过限制去细微地操作具体分数。这可以被看做是SVM的一种特性。举例说来,一个汽车的分类器应该把他的大量精力放在如何分辨小轿车和大卡车上,而不应该纠结于如何与青蛙进行区分,因为区分青蛙得到的评分已经足够低了。
Softmax实现:
<li>softmax.py
import numpy as np
from random import shuffle
import math
def softmax_loss_naive(W, X, y, reg):
"""
Softmax loss function, naive implementation (with loops)
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in xrange(num_train):
scores = X[i].dot(W)
scores = np.exp(scores)
scores = normalized(scores)
for j in xrange(num_classes):
if j == y[i]:
continue
margin = -np.log(scores_correct)
if margin > 0:
loss += margin
dW[:, y[i]] += -X[i, :]
dW[:, j] += X[i, :]
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
dW += reg * W
return loss, dW
def softmax_loss_vectorized(W, X, y, reg):
"""
Softmax loss function, vectorized version.
Inputs and outputs are the same as softmax_loss_naive.
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
scores = X.dot(W)
scores = np.exp(scores)
scores = normalized(scores)
num_classes = W.shape[1]
num_train = X.shape[0]
margins = -np.log(scores)
ve_sum = np.sum(margins,axis=1)/num_classes
y_trueClass = np.zeros_like(margins)
y_trueClass[range(num_train), y] = 1.0
loss += (np.sum(ve_sum) / num_train)
dW += np.dot(X.T,scores-y_trueClass)/num_train
return loss, dW
def normalized(a):
sum_scores = np.sum(a,axis=1)
sum_scores = 1 / sum_scores
result = a.T * sum_scores.T
return result.T
测试:
不同参数下Softmax的识别率结果:

总结:
本章主要介绍了另一个线性分类器Softmax,阐述了Softmax与SVM的主要区别,而Softmax的loss function对于以后的神经网络的学习有很大的帮助。