一、什么是堆?
- 首先是一棵完全二叉树;
- 大顶堆:每个结点的值都大于或等于其左右孩子结点的值;
- 小顶堆:每个结点的值都小于或等于其左右孩子结点的值;
-
根结点一定是堆中所有结点最大或最小;
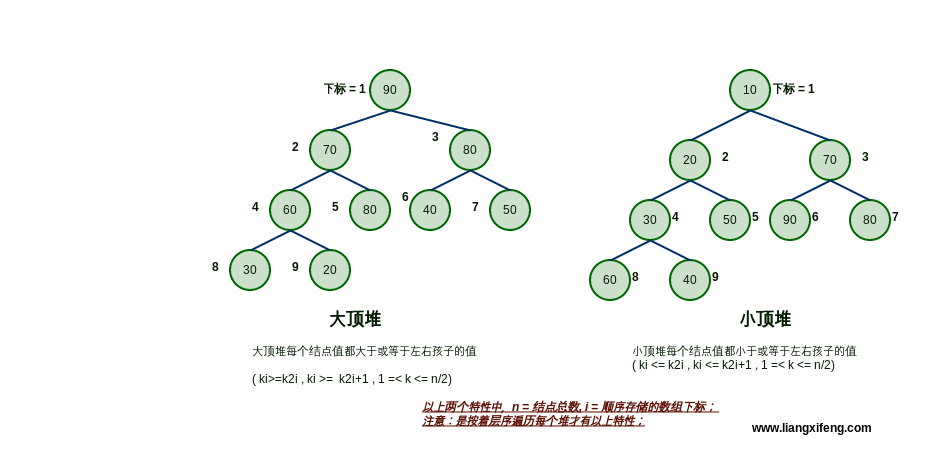 heap
heap
二、堆排序(Heap Sort)
- 将待排序的序列构成一个大(小)顶堆,然后根据堆的性质,每次将堆顶元素(根结点)输出作为呆排序有序序列的元素,然后调整剩余元素成为新的堆,反复的操作直到堆中所有元素全部输出,最终得到一个有序序列;
- 一颗有n个节点的完全二叉树,对其任意节点i,原则如下:
- 如果i=1,则为根节点,无双亲
- 如果2i>n,则节点i没有左孩子
- 如果2i+1>n,则节点i没有右孩子
以下内容借用 勇哥的分析
其实堆在内存中还是采用原来的数组存储,只不过是在交换元素之间的位置,下面我们一边看代码实现(借用大话数据结构的代码)
三、代码分析
堆排序 = 数组预处理(堆)+ 排序(swap)
<img src="https://raw.githubusercontent.com/liangxifeng833/my_program/master/images/datastruct/sort-heap-2.png" width="600" />
要排序的队列是{50,10,90,30,70,40,80,60,20},这段代码就是我们说的,通过堆将数组的最大值处理到数组的下标1的位置上,然后用swap函数(排序)取走(这里它是交换到最后一个位置),然后再用堆将数组重新处理,等待下一次比对!
这里又出现了新问题,为什么预处理的时候,循环是从L->lenth/2开始的????
看看下面这张图,在没有形成堆前,我们可以把这个数组看成这棵树,循环的次数就是这棵树的层数,看看四个灰色节点和其叶子节点的值就能找到规律
也就是:
- s=>30, 2*s=>60, 2*s+1=>20
- s=>90, 2*s=>40, 2*s+1=>80
- s=>10, 2*s=>30, 2*s+1=>70
- s=>50, 2*s=>10, 2*s+1=>90
根据这个规律,s从L->length/2开始,自下而上的求每个子树的最大值,然后换至根节点(子树),然后这个子树根节点又会成为上一层节点的孩子节点
<img src="https://raw.githubusercontent.com/liangxifeng833/my_program/master/images/datastruct/sort-heap-3.png" width="300" />
最后代码实现就是下面这张图,可以看到里面写了注释,其实就是自下而上,自右至左的按照刚才那棵树的位置,将最大值一步步的换到根节点的过程。
<img src="https://raw.githubusercontent.com/liangxifeng833/my_program/master/images/datastruct/sort-heap-4.png" width="600" />
在每次swap将最小值交换至下标1的位置上后,调用HeapAdjust函数,只需要对第一层,也就是根节点进行调整,即可完成处理!!!!
<img src="https://raw.githubusercontent.com/liangxifeng833/my_program/master/images/datastruct/sort-heap-5.png" width="400" />