日期:20160310
注: 本人缺乏风工程基础,本篇笔记难免有错误之处。
引言
结构风灾害案例:
- 日本明港西大桥拉索风雨振;
- 东京港大桥振动;
- Tacoma Narrows Bridge颤振破坏;

结构对象
对风敏感的结构:
- 桥梁,大跨度悬索桥、斜拉桥;
- 高层高耸结构;
- 大跨(索膜)结构;
- 风能发电结构(海洋+陆地);
- 输电结构(电塔+电线)
- 海洋结构
- 海洋平台
- 输油管道
这些结构的共同特点是:
- 柔度大,基频低;
- 阻尼比小;
在实际的振动问题中,阻尼的影响可能比频率f更大。
研究的视野要宽广,不要只局限于建筑结构,还应该看到桥梁、电力、能源的应用。
风振基本问题
动力学基本方程如下:
\begin{equation}
m \ddot{x} + c \dot{x} + kx = F(t)
\end{equation}
在地震工程中$F(t) = m \ddot{x}_g$,在风工程中$F(t)$即为风压荷载。在不同的风速下风压荷载的形式不同:
- 脉动风,时变;
- 层流风,定常;
由于绕流场不同,风荷载模型的表达形式不同,普遍的隐式表达式;
\begin{equation}
F = F(u,I,L,A,S,t)
\end{equation}
其中:
- u--风速;
- L--结构尺度;
- t--时间;
- 其余参数含义不懂;
绕流场的影响因素:
- 结构的形状;
- 流固耦合作用;
国内研究机构
- 同济大学,桥梁抗风,项海帆院士在80年代初创建风洞;
- 西南交大,铁路桥梁风工程;
- 哈工大-大跨空间结构组,大跨结构风工程的关键在于结构形状复杂,孙瑛老师创建风荷载试验数据库系统;
- 哈工大-深圳研究生院,高层结构抗风研究;
哈工大放在课题组(Structure Monitoring Cneter,SMC)起步较晚,其他机构普遍关注于风荷载$F(t)$的研究,SMC选择了更深层的流场研究和健康监测作为战略方向:
- 研究流场,分析风荷载的形成;
一般的风洞试验主要测试风压为结构设计提供依据; - 桥梁风振监测;
首次将PIV粒子成像系统应用于风工程(陈文礼教授,高东来博士);
常见振动的形式
风致振动的主要形式有5种:
- 涡振,东京港大桥高层结构;
- 颤振,Tacoma Narrows Bridge;
- 风雨振,斜拉桥拉索;
- 抖振,所有结构普遍存在;
- 弛振
- 单纯弛振
- 尾流弛振(输电线);
风荷载的形式影响振动系统的性质:
- $F(t)$,荷载仅与时间相关,则系统为线性系统,与典型的结构动力学模型一样;
- $F(t,y,y^{'},yx)$,荷载与结构振动状态耦合,形成非线性系统,不满足叠加原理
涡振
涡振由层流风(定常,无脉动)引起,当尾流漩涡脱落时的频率与结构自振频率相等$f_v = f_c$,激发结构横向振动。示意图如下:
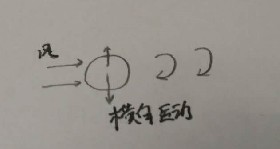
振动特点:
- 限幅振动;
- 滞回现象;
- 群体效应;
限幅振动
在非线性动力学中,阻尼与位移加速度相关,即$c = c(y,y^{'})$。在小位移,低速度的状态下,风的动能输入使得$c<0$,负阻尼,振幅不断加大;当振动达到临界状态$ c=0 $,0阻尼情况下,结构自由振动,振幅不变。
总阻尼 = 固体阻尼 + 气动阻尼
滞回现象
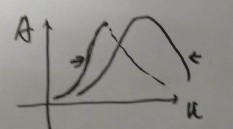
如图
- 风速增大,振幅增大到一定程度,然后消失;
- 风速减小,振幅先增大后减小,但与风速增大过程的曲线不同;
即相同的风速下可能处于不同的振动状态。
群体效应
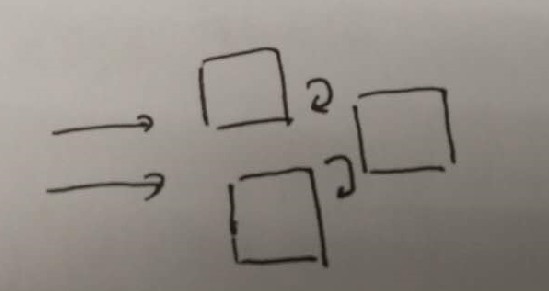
多栋建筑距离较近时,风场形成的涡流相互影响。
案例

双箱梁的截面设计本来为了减少颤振(事实上的确减小了颤振),但引起了涡振,双箱之间形成涡流。
风洞模型试验没有发现涡振,这很可能是模型阻尼小造成涡振差别很大。
模型与实桥的雷诺数Re差别很大:
- 实际$10^8$
- 模型$10^5$
此为一大研究难题。
颤振
颤振,即导致Tacoma Narrows Bridge破坏的振动形式,是桥梁设计的控制因素,规范严格控制颤振。
涡振与颤振均由层流风引起:
- 低风速(4m/s-12m/s),涡振
- 高风速(12m/s-50m/s),颤振
国内测量的最高风速为100m/s,颤振设计临界风速一般为65m/s。
颤振的研究分为3个时期:
- 30-70年代;
- 80 年代;
- 80-至今;
30-70年代
主要研究航空领域机翼的颤振,机翼为平板结构不能直接应用于桥梁结构。
桥梁的气动断面主要有:
-
桁架,美国日本多采用;
 桁架梁-明石海峡大桥
桁架梁-明石海峡大桥 -
箱梁,欧洲中国多采用;
 箱梁-南京长江二桥
箱梁-南京长江二桥
桁架梁结构可以看做上下2片平板,直接采用机翼颤振理论;
箱梁的颤振气动自激力模型由 Robert H. Scanlan(The Johns Hopkins University霍普金斯大学)提出,假设单模态颤振。
80 年代
考虑桥梁结构跨度越来越大,高层建筑越来越高,结构跨越不同的风场,故研究多模态颤振模型。
80-至今
发现颤振的2种类型
- 硬颤振,很快导致结构破坏;
- 软颤振,不会快速破坏;
两者在气动自激力有差别。
抖振
抖振由脉动风引起,采用结构随机振动理论求解。
- 风荷载->脉动风速谱;
- 由伯努利方程将风速转换为风压;
- 加载,求解;
抖振理论由Alan G. Davenport(Canada,风工程专家、边界层风洞创始人)在1972年创立:
- 流固耦合;
- 气动导纳函数;
- Sears函数;
有待研究点:
- 气动导纳;
- 结构体量很大时,不同部位启动特性的相关性;
- 考虑结构振动的气弹模型,目前试验普遍采用刚性模型;
风雨振
在一定的风雨组合下,雨水在斜拉索表面形成水线,改变拉索的气动外形,引发强烈振动。可以在斜拉索表面加螺旋线,防止水线形成,控制振动,但机理尚不清楚。
弛振
在一定的风攻角,圆截面的构件迎风面实际变成椭圆,引发弛振。
研究方法
- 风洞试验;
- 数值计算;
- 现场监测;
- 理论研究;
- 风洞试验技术,陈文礼老师;
问题:
- 风雨振试验,难以测量表面风压,如果布置测试则破坏水线,无法形成风雨振;
- 风荷载较难在风洞实验室模拟重现;
- 大尺度涡流(500 m)难以在实验室制造,实验室尺度不超过20 m;
- 现场监测试验,流场的检测困难;
- 高雷诺数($Re = 10^8$)的数值求解问题,无法忽略小涡的影响;
应用
- 烟囱效应:高层结构内外温度、气压差别较大,风声很大,电梯门关不住;
- 测试风场分布,确定风能最大的地方,建立风力发电站;