曾梓龙 材料班 2014301020006

前言

最近的研究课题是神经网络，偶然在知乎上看到了一篇关于入门深度学习的文章,介绍了一下从数学知识到机器学习，再到神经网络和深度学习的资源，因此开始通过看Andrew Ng的机器学习课程入门机器学习，并在网上在线看Neural Networks and Deep Learning这份线上教程学习神经网络和深度学习。

在花了几天时间看线上教程，我开始着手操作识别手写数字图像的任务，为了简化代码，我使用python构建神经网络。

背景

首先观察下面的一副图片

我们可以很容易地辨识这些数字是504192。通过对大脑的研究，我们知道，人类大脑有大约1000亿个神经元，在这些神经元之间有一万亿个链接。

而在大脑的每个半球，人类有一个初级视觉皮层V1，大概有1.4亿个神经元，以及数百亿的相互连接，但是人类视觉不仅涉及V1，而且还有V2，V3，V4，V5这一系列的视觉皮层。

实际上，人类大脑就是一台超级计算机，几百万年来的调整和适应使得人类能够辨识外部世界，因此用计算机模拟书写数字是很艰难的。

这里有一个问题值得思考。为什么我们能够辨识手写数字9？是因为我们天生就能够辨识数字9还是因为我们学习过如何辨识数字9？

答案显然是我们学习过如何辨识并书写数字9.

从这个问题出发来看，我们也可以用计算机模拟人类学习的过程来获得辨识手写数字图像的能力。

近年来，神经网络在这类问题的解决上取得了比较大的进展。而神经网络模拟的就是人类大脑的工作方式——使用大量的训练数据训练神经网络，使神经网络的从这些数据中获取“经验”，提高辨识手写数字图像的准确率。

何为神经网络以及神经网络的工作原理

Perceptrons（感知器）

在介绍神经网络之前，我们首先需要理解Perceptrons(感知器)的概念。Perceptrons实际上就是一个人工模拟的神经元，每个感知器有若干个二进制输入以及一个二进制输出。

上面的这个Perceptrons有三个输入：x1、x2和x3，每条输入都有相应的权重:w1、w2和w3.

Perceptrons的输入是由输入的加权之和决定的，神经网络的研究人员通常用下面的这个公式来确定Perceptrons的输出：


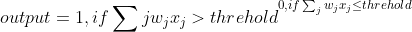
也就是说，当Perceptrons的输入加权和大于某一阈值时，输出1；小于某一阈值时输出0.

这和大脑神经元的工作原理比较类似，当神经元接收到来自其他神经元的信号时，经过处理之后再发送给其他的神经元。

在实际应用中，为了计算方便，我们将上面的式子改为：


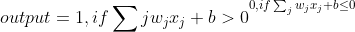
其中：

b为bias.

同时令X为输入数据的矩阵，W为相应的权重矩阵，即：

因此输出表达式为：


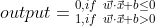
我们在之前也说过，人类大脑识别图像是通过多层的视觉皮层来解析的信息，因此我们这里开始构建一个三层的神经网络：

第一层称为输入层，最后一层称为输出层，第一层和最后一层之间的层被称为隐藏层。

我们首先考虑一下这样一个Perceptrons，有两个输入端，每个输入端的权重为-2，结点bias为3：

如果我们输入00，则有：
(-2)0+(-2)0+3 = 3>0,类似的，输入为01或者10时输出都为1，但是当输入为11时，输出为0，因此这样的一个Perceptrons可以看作一个与非门。

在数字逻辑中，我们知道，逻辑门的组合可以组成一定的逻辑开关，如下图所示：

将上图中的与非门换成之前讨论的Perceptrons，则有：

减少一些线条，并将输入端转换为Perceptrons，则有：

从上面的例子可以看到，不同的Perceptrons的组合网络可以具有一定的逻辑功能，利用神经网络识别手写数字也是一样的原理。

Sigmod 神经元

在实际应用中，并不会使用之前介绍的Perceptrons组成的神经网络，那样构建的神经网络不够稳定，在使用训练集训练网络的时候网络权重、bias甚至网络的输出的变化非常大。因此，往往使用Sigmod神经元。

Sigmod神经元里的Perceptrons和之前的Perceptrons并无两样，但是Perceptrons的输出output的值并非0或1，相反，output 为：

)
其中σ称为sigmoid函数，sigmoid函数定义如下：
\equiv \frac{1}{1+e^{-z}}.)

因此对于输入为x1,x2,...,输入权重为w1,w2,...,且bias为b时，sigmoid神经元的输出为：

sigmoid函数σ(z)的图像如下图所示：

当z大于0时，sigmoid函数小于1大于0.5，当z小于0时，sigmoid函数大于0小于0.5.

这是之前刚开始介绍的Perceptrons的输出函数(Step function)的图像

sigmoid function与step function相比更为平滑，当权重w、bias b有微小变化时，sigmoid函数的输出的变化也很微小。因此一般采用sigmoid函数作为输出函数。

从sigmoid函数图像可以看到，sigmoid函数的输出是连续变化的，可能是0.173或者0.689，那么如何界定sigmoid的输出值以确定output值？
我们一般界定，当sigmoid函数大于0.5时output为1，当sigmoid函数小于0.5时，output为0

识别手写数字的神经网络搭建

首先，我们识别一个手写数字：

为了识别单个数字，我们使用一个三层的神经网络：

由于我们的手写数字是一个28*28的像素的图像，因此手写数字图像中一共有784个像素，这些像素块经过编码后输入到神经网络中，因此这个三层神经网络的输入端有784个神经元。

输入端值为1时代表像素块为1，值为0时代表像素块为白色，当输入端值介于0到1之间时，代表深度不同的灰色。

第二层也就是隐藏层，在图中仅有15个神经元，不过在实际情况中有可能不只15个神经元。

第三层也就是输出层，有十个神经元，如果哪个神经元输出为1，则代表神经网络认定输入的图像为相应的数字。例如，如果第一个神经元输出为1，则神经网络认定输入的手写数字为0.

梯度下降算法

之前我们说过，神经网络可以通过训练数据集来获得辨识图像的能力，其模拟的就是人类的学习能力，在这里我们提出一个梯度下降学习算法模拟学习的过程。

我们使用向量x表示输入的值，则x是一个784维度的向量，输入端用y表示，则有

)

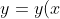其中，y是一个10维的向量。
举个例子来说，如果一个训练图像被神经网络认定为6，则

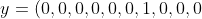^T)
就是神经网络的输出向量。

为了不断调整神经网络内的权重和bias，我们提出梯度下降算法，首先定义一个代价函数：
 \equiv \frac{1}{2n}\sum_x ||y(x)-a||^2)

其中w为神经网络中所有的权重值，b为所有的bias，n为输入的训练集的数量，a是当输入为x时神经网络的输出向量。由此可见，w、b和n为a的自变量。

如上图为代价函数C(w,b)的等势图，中心处为代价函数图像的最低点，越往外，点所处的位置越高。因此为了求得代价函数C的极小值，我们需要找到相应代价函数的图像的最低点。

更直观一点就像上面这幅图所示，小球处于某一位置，总有向最低点运动的趋势。为了在数学语言上描述这一过程，我们提出梯度下降算法：
令：
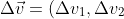^T)

)
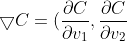有：

因为代价函数需要沿梯度下降，所以应当有
令：
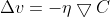
其中，η是一个很小的正参数：


更新参数v，有：

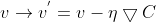
因此，分别更新权重w和偏重b：

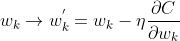
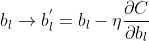
但是在实际情况中，使用梯度下降学习算法训练神经网络效率比较低，因此我们采用随机梯度下降学习算法。

随机梯度下降学习算法的基本思想是在所有训练集中随机挑选m个训练集输入到神经网络中进行训练，m足够大以至于可以认为这m个训练集的训练效果相当于所有训练集训练神经网络的效果，用数学公式表达就是：
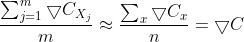
也就是说，w与b的更新函数可以改为：

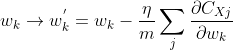
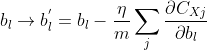
编程实现

先建立一个Network类：

class Network(self):
    def __init__(self,sizes):

        self.num_layers = len(sizes)
        self.sizes = sizes
        # if we want to create a Network object with 2 neurons 
        # in the first layer,3 neurons in the second layer,and
        # 1 neurons in the final layer,we can do this in this 
        # code:
        # net = Network([2,3,1])
        self.biases = [np.random.randn(y,1) for y in sizes[1:]]
        self.weights = [np.random.randn(y,x) 
                        for x,y in zip(sizes[:-1],sizes[1:])]

我们建立的是一个三层的神经网络，传入一个三维的向量,例如：
如果我们想在输入层放入2个神经元，隐藏层放入3个神经元，输出层放入1个神经元，则将[2,3,1]传入神经网络中。

net = Network([2,3,1])

biases和weight则先用random函数初始化，随机设置。

定义sigmoid函数：

def sigmod(z):
    return 1.0/(1.0+np.exp(-z))

每一层神经元的输出由上一层神经元的输入决定，由数学公式表达就是：

其中，a是上一层神经元的输出，即这一神经元的输入，w是相应两层神经元之间的权重向量。

同时在Network类中定义feedforward方法：

def feedforward(self,a):
        for b,w in zip(self.biases,self.weights):
            a = sigmod(np.dot(w,a)+b)
        return a

同时在Network类中定义SGD方法，SGD方法使神经网络能够使用随机梯度下降算法进行学习：

    def SGD(self,training_data,epochs,mini_batch_size,eta,test_data=None):
        # epochs:the number of epochs to train for
        # mini_batch_size:the size of the mini-batches to use
        # when sampling.eta is the learning rate /eta.
        if test_data:
            n_test = len(test_data)
        n = len(training_data)
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0,n,mini_batch_size)]
            # catch k in every mini_batch_size
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch,eta)
            if test_data:
                print("Epoch {0}:{1}/{2}".format(j,self.evaluate(test_data),n_test))
            else:
                print("Epoch {0} complete".format(j))   

在之前讨论随机梯度下降学习算法的时候，我们谈到w与b要随神经网络的学习不断更新，在这里定义一个update_mini_batch方法：

def update_mini_batch(self,mini_batch,eta):
        # update the network's weights and biases by applying gradient
        # descent using backpropagation to a single mini batch
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x,y in mini_batch:
            delta_nabla_b,delta_nabla_w = self.backprop(x,y)
            nabla_b = [nb+dnb for nb,dnb in zip(nabla_b,delta_nabla_b)]
            nabla_w = [nw+dnw for nw,dnw in zip(nabla_w,delta_nabla_w)]
        self.weights = [w-((eta)/len(mini_batch))*nw
                        for w,nw in zip(self.weights,nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                        for b,nb in zip(self.biases,nabla_b)]

完整代码已经托管到github上了。
在使用神经网络的时候，还需要一个python文件将训练集输入到神经网络中，我使用了国外某大佬的mnist_loader.py文件，也托管在github上了。

运行操作

打开python shell，切换到程序文件目录，输入下列代码：

在进入python交互环境之后，第一行和第二行代码导入了训练集，第三行和第四行代码创建了一个第一层为784个神经元 第二层为30个神经元 第三层为10个神经元的神经网络。

再输入下列这行代码启动神经网络：

net.SGD(training_data,30,10,3.0,test_data=test_data)

这行代码的意思是训练30次，同时挑选10组训练集作为随机梯度下降算法的训练集，学习速率η为3.0，运行一段时间后，得到：

经过30次训练之后，神经网络辨识图像的准确度可以达到94.89%,实际上在第28次训练的时候准确度已经达到了94.99%.

如果我们将这个神经网络的第二层改为100个神经元，神经网络的辨识度可以达到多少？
输入下列代码：

net = network.Network([784,100,10])

启动神经网络，我们可以将神经网络的辨识率提高到96%以上。

重新回到第二层为30个神经元的情况上，如果将学习速率η提高到20的话，将程序运行一遍得到：

可以发现，神经网络辨识图像的准确率有所下降。

总结

训练神经网络所需的计算量十分巨大，用普通的笔记本运行整个程序需要花费比较长的一段时间，因此，在实际应用中一般采用GPU来训练神经网络。在实际模拟的过程中，我们可以发现，神经网络的辨识率虽然可以提高到95%以上，但是在这之后其辨识率很难得到提高，这迫使我们不断发展神经网络模型。